Numerické metódy matematiky I
|
|
|
- Γοργοφόνη Ανδρέου
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Prednáška č. 7 Numerické metódy matematiky I Riešenie sústav lineárnych rovníc ( pokračovanie )
2 Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc ako neznámych SVD pre viac rovníc ako neznámych 2. QR-rozklad 3. Literatúra
3 Terminológia a základné vzťahy Majme štvorcovú maticu A. Jej vlastné čísla budeme označovať λ n a pravé resp. ľavé vektory x a y, Ak platí, že pre ktoré platí A potom λ i, x i y i a je symetrická, vlastné vektory generujú ortogonálnu bázu. Podobnostná transformácia P -1 AP nemení vlastné čísla matice A. det A λi 0 Ax λ x i i i T T i λiyi y A a
4 Terminológia a základné vzťahy Reálna ortogonálna matica je taká štvorcová matica Q, ktorej transponovaná matica je jej inverznou maticou. T T Q Q QQ I Ak Q je obdĺžniková matica, potom podmienky T Q Q I a QQ I nie sú ekvivalentné. T Podmienka Q T.Q = I hovorí, že matica Q je stĺpcovo ortogonálna. Podmienka Q.Q T = I hovorí, že matica Q je riadkovo ortogonálna.
5 Metóda singulárneho rozkladu - úvod Ak je počet rovníc sústavy M menší ako počet neznámych N, alebo ak M = N ale rovnice sú lineárne závislé, potom sústava nemá žiadne riešenie alebo má viac než jedno riešenie. V druhom prípade priestor riešení tvorí partikulárne riešenie pripočítané k ľubovoľnej lineárnej kombinácii N - M vektorov. Úlohu nájsť priestor riešení matice A je možné riešiť metódou singulárneho rozkladu matice A.
6 Metóda singulárneho rozkladu - úvod Ak je počet rovníc sústavy M väčší ako počet neznámych N, vo všeobecnosti neexistuje vektor riešenia a sústave rovníc sa hovorí preurčená. Môžeme ale nájsť najlepšie kompromisné riešenie, ktoré je najbližšie k tomu, aby vyhovovalo všetkým rovniciam. Ak najbližšie definujeme v zmysle najmenších štvorcov, t.j. že suma kvadrátu rozdielov medzi ľavou a pravou stranou rovnice je najmenšia, potom sa preurčený systém redukuje na (zvyčajne) riešiteľný problém zvaný metóda najmenších štvorcov.
7 Metóda singulárneho rozkladu - úvod Redukovaný systém rovníc môžeme zapísať ako systém N x N rovníc T T A A x A b. Tieto rovnice voláme normálne rovnice problému najmenších štvorcov. Metóda singulárneho rozkladu má veľa spoločného s problémom najmenších štvorcov, čo si ukážeme neskôr. Priame riešenie normálnych rovníc nie je vo všeobecnosti najlepším spôsobom hľadania riešenia najmenších štvorcov.
8 Metóda singulárneho rozkladu V mnohých prípadoch, keď GEM alebo LU rozklad zlyhajú, metódy singulárneho rozkladu (singular value decompisition, SVD) presne diagnostikujú, v čom je problém a v mnohých prípadoch tiež poskytnú vhodné numerické riešenie. SVD je tiež metóda na riešenie mnohých problémov najmenších štvorcov.
9 Metóda singulárneho rozkladu SVD je založená na nasledujúcej teoréme lineárnej algebry: Každá matica A typu M x N, ktorej počet riadkov M je väčší alebo rovný počtu stĺpcov N, môže byť zapísaná ako súčin stĺpcovo-ortogonálnej matice U typu M x N, diagonálnej matice W typu N x N s kladnými alebo nulovými prvkami (singulárnymi hodnotami) a transponovanej ortogonálnej matice V typu N x N.
10 Metóda singulárneho rozkladu Ortogonálnosť matíc U a V môžeme zapísať nasledovne
11 Metóda singulárneho rozkladu SVD dekompozícia môže byť vykonaná aj keď M < N. V takom prípade singulárne hodnoty w j sú všetky nulové pre j = M+1,, N ako aj odpovedajúce stĺpce matice U. Existuje viacero algoritmov na SVD, osvedčená je subroutina svdcmp z Numerical Recipes.
12 Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc ako neznámych SVD pre viac rovníc ako neznámych 2. QR-rozklad 3. Literatúra
13 Metóda singulárneho rozkladu štvorcovej matice Aj je matica A štvorcová, povedzme typu N x N, potom U, W a V sú všetko štvorcové matice typu N x N. Keďže U a V sú ortogonálne, ich inverzné matice sú rovné ich transponovaným maticiam. Potom môžeme písať vzťah pre inverznú maticu A A 1 diag 1/ T V U w j SVD dáva jasnú diagnostiku situácie, ak sú niektoré singulárne hodnoty nulové alebo blízke nule.
14 Metóda singulárneho rozkladu štvorcovej matice Norma matice A A max Ax max UwV x x 1 x 1 T
15 Metóda singulárneho rozkladu štvorcovej matice Norma matice A A max Ax max UwV x x 1 x 1 keďže pre Euklidovskú normu platí, že T T U Ux Ux
16 Metóda singulárneho rozkladu štvorcovej matice Norma matice A A max Ax max UwV x x 1 x 1 keďže pre Euklidovskú normu platí, že T T U Ux Ux T potom A max wv x max wy max x 1 y 1 w j
17 Metóda singulárneho rozkladu štvorcovej matice Norma matice A A max A x max Vw U x x 1 x 1 T
18 Metóda singulárneho rozkladu štvorcovej matice Norma matice A A max A x max Vw U x x 1 x 1 podobne potom 1 1 T 1 A max w U x max w y min x 1 y 1 T w 1 j
19 Metóda singulárneho rozkladu štvorcovej matice Pripomeňme jednu z definícií čísla podmienenosti matice κ(a): κ A : A A 1 max min w w j j Matica je singulárna ak je jej číslo podmienenosti nekonečno. Matica je zle podmienená ak prevrátená hodnota jej čísla podmienenosti je blízka strojovej presnosti počítača, t.j. menšia než 10-6 pre jednoduchú presnosť alebo pre dvojnásobnú presnosť.
20 Metóda singulárneho rozkladu štvorcovej matice Prípad sústavy lineárnych rovníc Ax b v ktorej matica A je singulárna:, Najskôr sa pozrime na prípad homogénnej sústavy, t.j. prípad keď b=0. Inými slovami hľadáme nulový priestor A
21 Metóda singulárneho rozkladu štvorcovej matice Prípad sústavy lineárnych rovníc Ax b v ktorej matica A je singulárna:, Najskôr sa pozrime na prípad homogénnej sústavy, t.j. prípad keď b=0. Inými slovami hľadáme nulový priestor A n : n T : null A x Ax 0 x UwV x 0 n T T : n T x U UwV x 0 x : wv x 0
22 Metóda singulárneho rozkladu štvorcovej matice Prípad sústavy lineárnych rovníc Ax b v ktorej matica A je singulárna:, Najskôr sa pozrime na prípad homogénnej sústavy, t.j. prípad keď b=0. SVD dáva priamo riešenie každý stĺpec matice V, ktorého zodpovedajúca singulárna hodnota w j je nulová je riešením.
23 Metóda singulárneho rozkladu štvorcovej matice Prípad sústavy lineárnych rovníc Ax b v ktorej matica A je singulárna:, Teraz sa pozrime aký je rozsah (range) matice A
24 Metóda singulárneho rozkladu štvorcovej matice Prípad sústavy lineárnych rovníc Ax b v ktorej matica A je singulárna:, Teraz sa pozrime aký je rozsah (range) matice A : n T : n : n range A Ax x UwV x x Uwy y T y V x
25 Metóda singulárneho rozkladu štvorcovej matice Prípad sústavy lineárnych rovníc Ax b v ktorej matica A je singulárna:, Teraz sa pozrime aký je rozsah (range) matice A Range matice A je tvorený obalom (span) stĺpcov matice U, ktorých zodpovedajúca singulárna hodnota w j je nenulová.
26 Metóda singulárneho rozkladu štvorcovej matice Hľadané riešenie systému s nenulovou pravou stranou pomocou SVD nájdeme nasledovne: nahradíme 1/w j nulou ak w j =0 potom počítame (sprava doľava) x V diag 1/ U b T w j Ak partikulárne riešenie leží v rozsahu (range) A, 2 potom má najmenšiu veľkosť x. Ak partikulárne riešenie neleží v rozsahu (range) A, r : Ax b potom x minimalizuje rezíduum riešenia.
27 Metóda singulárneho rozkladu štvorcovej matice Matica A nie je singulárna
28 Metóda singulárneho rozkladu štvorcovej matice Matica A je singulárna
29 Metóda singulárneho rozkladu štvorcovej matice Doteraz sme uvažovali len o krajných prípadoch a to že matica sústavy je alebo nie je singulárna. Numericky je častý prípad, že singulárne hodnoty w j sú veľmi malé, no nenulové, takže matica je zle podmienená. V takom prípade môžu priame metódy poskytnúť formálne riešenie, ale vektor riešenia má nezmyselne veľké prvky, ktoré pri algebraickom krátení počas násobení maticou A dajú veľmi zlú aproximáciu vektora pravej strany. Vtedy je často lepšie malé hodnoty w j vynulovať a riešenie určiť podľa vzorca (s tým, že 1/w j nahradíme nulou ak w j =0) x diag 1/ T V w j U b Je nutné byť ale opatrný a dobre zvoliť prahovú hodnotu nulovania veličín w j
30 Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc ako neznámych SVD pre viac rovníc ako neznámych 2. QR-rozklad 3. Literatúra
31 Metóda singulárneho rozkladu pre menej rovníc ako neznámych Ak máme menej rovníc ako neznámych neočakávame jediné riešenie. Obyčajne existuje celý N - M rozmerný priestor riešení, ktorý chceme nájsť. SVD dá v takomto prípade N - M nulových alebo zanedbateľne malých hodnôt w j. Ak niektoré z M rovníc degeerujú, môžeme získať ďalšie nulové w j. Potom tie stĺpce matice V, ktorých zodpovedajúca singulárna hodnota w j je nulová tvoria bázové vektory hľadaného priestoru riešení. Partikulárne riešenie nájdeme aplikovaním vzorca x V diag 1/ U b T w j
32 Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc ako neznámych SVD pre viac rovníc ako neznámych 2. QR-rozklad 3. Literatúra
33 Metóda singulárneho rozkladu pre viac rovníc ako neznámych Ak máme viac rovníc ako neznámych hľadáme riešenie, v zmysle problému najmenších štvorcov. Riešime teda sústavu, zapísanú tabuľkovo nasledovne:
34 Metóda singulárneho rozkladu pre viac rovníc ako neznámych Po aplikácii SVD na maticu A dostaneme riešenie v tvare V tomto prípade nie je zvyčajne nutné nulovať hodnoty w j avšak neobvykle malé hodnoty indikujú, že dáta nie sú citlivé na niektoré parametre.
35 Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc ako neznámych SVD pre viac rovníc ako neznámych 2. QR-rozklad 3. Literatúra
36 QR rozklad Podobne ako LU rozklad matice, existuje aj tzv. QR rozklad matice A = Q.R kde R je horná trojuholníková matica a Q je ortogonálna matica, teda platí Q T.Q = 1. Riešenie sústavy rovníc nájdeme riešením R.x = Q T.b QR rozklad vyžaduje asi 2-krát viac operácií ako LU rozklad, ale existujú špeciálne typy rovníc, v ktorých je výhodnejšie ho použiť.
37 Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc ako neznámych SVD pre viac rovníc ako neznámych 2. QR-rozklad 3. Literatúra
38 Literatúra
39 Literatúra
40 Literatúra
Úvod do lineárnej algebry. Monika Molnárová Prednášky
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
x x x2 n
 Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
15. Matlab Lineárna algebra
 1 Portál pre odborné publikovanie ISSN 1338-0087 15. Matlab Lineárna algebra Blaho Michal MATLAB/Comsol 18.09.2009 Matlab pracuje s dátami vo forme vektorov a matíc. Základnej práci s vektormi a maticami
1 Portál pre odborné publikovanie ISSN 1338-0087 15. Matlab Lineárna algebra Blaho Michal MATLAB/Comsol 18.09.2009 Matlab pracuje s dátami vo forme vektorov a matíc. Základnej práci s vektormi a maticami
Riešenie sústavy lineárnych rovníc. Priame metódy.
 Riešenie sústavy lineárnych rovníc. Priame metódy. Ing. Gabriel Okša, CSc. Matematický ústav Slovenská akadémia vied Bratislava Stavebná fakulta STU G. Okša: Priame metódy 1/16 Obsah 1 Základy 2 Systémy
Riešenie sústavy lineárnych rovníc. Priame metódy. Ing. Gabriel Okša, CSc. Matematický ústav Slovenská akadémia vied Bratislava Stavebná fakulta STU G. Okša: Priame metódy 1/16 Obsah 1 Základy 2 Systémy
Motivácia Denícia determinantu Výpo et determinantov Determinant sú inu matíc Vyuºitie determinantov. Determinanty. 14. decembra 2010.
 14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
Matematika Funkcia viac premenných, Parciálne derivácie
 Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR. Michal Zajac. 3 T b 1 = T b 2 = = = 2b
 VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR Michal Zajac Vlastné čísla a vlastné vektory Pripomeňme najprv, že lineárny operátor T : L L je vzhl adom na bázu B = {b 1, b 2,, b n } lineárneho priestoru L určený
VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR Michal Zajac Vlastné čísla a vlastné vektory Pripomeňme najprv, že lineárny operátor T : L L je vzhl adom na bázu B = {b 1, b 2,, b n } lineárneho priestoru L určený
Metódy vol nej optimalizácie
 Metódy vol nej optimalizácie Metódy vol nej optimalizácie p. 1/28 Motivácia k metódam vol nej optimalizácie APLIKÁCIE p. 2/28 II 1. PRÍKLAD: Lineárna regresia - metóda najmenších štvorcov Na základe dostupných
Metódy vol nej optimalizácie Metódy vol nej optimalizácie p. 1/28 Motivácia k metódam vol nej optimalizácie APLIKÁCIE p. 2/28 II 1. PRÍKLAD: Lineárna regresia - metóda najmenších štvorcov Na základe dostupných
1 Úvod Predhovor Sylaby a literatúra Základné označenia... 3
 Obsah 1 Úvod 3 1.1 Predhovor...................................... 3 1.2 Sylaby a literatúra................................. 3 1.3 Základné označenia................................. 3 2 Množiny a zobrazenia
Obsah 1 Úvod 3 1.1 Predhovor...................................... 3 1.2 Sylaby a literatúra................................. 3 1.3 Základné označenia................................. 3 2 Množiny a zobrazenia
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
MIDTERM (A) riešenia a bodovanie
 MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
Úvod do lineárnej algebry
 Katedra matematiky Fakulta elektrotechniky a informatiky Technická Univerzita v Košiciach Úvod do lineárnej algebry Monika Molnárová, Helena Myšková 005 RECENZOVALI: RNDr. Štefan Schrötter, CSc. RNDr.
Katedra matematiky Fakulta elektrotechniky a informatiky Technická Univerzita v Košiciach Úvod do lineárnej algebry Monika Molnárová, Helena Myšková 005 RECENZOVALI: RNDr. Štefan Schrötter, CSc. RNDr.
Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich
 Tuesday 15 th January, 2013, 19:53 Základy tenzorového počtu M.Gintner Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich násobenie reálnym číslom tak, že platí:
Tuesday 15 th January, 2013, 19:53 Základy tenzorového počtu M.Gintner Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich násobenie reálnym číslom tak, že platí:
Start. Vstup r. O = 2*π*r S = π*r*r. Vystup O, S. Stop. Start. Vstup P, C V = P*C*1,19. Vystup V. Stop
 1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
Goniometrické rovnice a nerovnice. Základné goniometrické rovnice
 Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Obvod a obsah štvoruholníka
 Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Ekvačná a kvantifikačná logika
 a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
Komplexné čísla, Diskrétna Fourierova transformácia 1
 Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
7. FUNKCIE POJEM FUNKCIE
 7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
Prechod z 2D do 3D. Martin Florek 3. marca 2009
 Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Vzorové príklady s riešeniami k lineárnej algebre a geometrie pre aplikovaných informatikov k písomke
 Vzorové príklady s riešeniami k lineárnej algebre a geometrie pre aplikovaných informatikov k písomke 23.5.26 Príklad č. Riešte sústavu Bx = r (B r) 2 3 4 2 3 4 6 8 8 2 (B r) = 6 9 2 6 3 9 2 3 4 2 3 2
Vzorové príklady s riešeniami k lineárnej algebre a geometrie pre aplikovaných informatikov k písomke 23.5.26 Príklad č. Riešte sústavu Bx = r (B r) 2 3 4 2 3 4 6 8 8 2 (B r) = 6 9 2 6 3 9 2 3 4 2 3 2
1 Polynómy a racionálne funkcie Základy Polynómy Cvičenia Racionálne funkcie... 17
 Obsah 1 Polynómy a racionálne funkcie 3 11 Základy 3 1 Polynómy 7 11 Cvičenia 13 13 Racionálne funkcie 17 131 Cvičenia 19 Lineárna algebra 3 1 Matice 3 11 Matice - základné vlastnosti 3 1 Cvičenia 6 Sústavy
Obsah 1 Polynómy a racionálne funkcie 3 11 Základy 3 1 Polynómy 7 11 Cvičenia 13 13 Racionálne funkcie 17 131 Cvičenia 19 Lineárna algebra 3 1 Matice 3 11 Matice - základné vlastnosti 3 1 Cvičenia 6 Sústavy
1. Limita, spojitost a diferenciálny počet funkcie jednej premennej
 . Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
. Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
Cvičenie č. 4,5 Limita funkcie
 Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
MATEMATIKA I. Doc. RNDr. Michal Šabo, CSc
 MATEMATIKA I Doc. RNDr. Michal Šabo, CSc 2 Obsah Predhovor 5 2 VYBRANÉ STATE Z ALGEBRY 2. Úvod................................... 2.2 Reálne n-rozmerné vektory...................... 2.3 Matice..................................
MATEMATIKA I Doc. RNDr. Michal Šabo, CSc 2 Obsah Predhovor 5 2 VYBRANÉ STATE Z ALGEBRY 2. Úvod................................... 2.2 Reálne n-rozmerné vektory...................... 2.3 Matice..................................
Matematika 2. Lineárna algebra. (ver )
 Matematika 2 Lineárna algebra (ver.01.03.2011) 1 Úvod Prehľad. Tieto poznámky obsahujú podklady k prednáške Matematika 2 na špecializácii Aplikovaná informatika: jedná sa o 12 dvojhodinových prednášok
Matematika 2 Lineárna algebra (ver.01.03.2011) 1 Úvod Prehľad. Tieto poznámky obsahujú podklady k prednáške Matematika 2 na špecializácii Aplikovaná informatika: jedná sa o 12 dvojhodinových prednášok
Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej transformácie,
 Kapitola Riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie, keď charakteritická rovnica má rôzne
Kapitola Riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie, keď charakteritická rovnica má rôzne
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
KATEDRA DOPRAVNEJ A MANIPULAČNEJ TECHNIKY Strojnícka fakulta, Žilinská Univerzita
 132 1 Absolútna chyba: ) = - skut absolútna ochýlka: ) ' = - spr. relatívna chyba: alebo Chyby (ochýlky): M systematické, M náhoné, M hrubé. Korekcia: k = spr - = - Î' pomerná korekcia: Správna honota:
132 1 Absolútna chyba: ) = - skut absolútna ochýlka: ) ' = - spr. relatívna chyba: alebo Chyby (ochýlky): M systematické, M náhoné, M hrubé. Korekcia: k = spr - = - Î' pomerná korekcia: Správna honota:
MATEMATIKA I ZBIERKA ÚLOH
 TECHNICKÁ UNIVERZITA V KOŠICIACH STAVEBNÁ FAKULTA ÚSTAV TECHNOLÓGIÍ, EKONOMIKY A MANAŽMENTU V STAVEBNÍCTVE KATEDRA APLIKOVANEJ MATEMATIKY RNDr. Pavol PURCZ, PhD. Mgr. Adriana ŠUGÁROVÁ MATEMATIKA I ZBIERKA
TECHNICKÁ UNIVERZITA V KOŠICIACH STAVEBNÁ FAKULTA ÚSTAV TECHNOLÓGIÍ, EKONOMIKY A MANAŽMENTU V STAVEBNÍCTVE KATEDRA APLIKOVANEJ MATEMATIKY RNDr. Pavol PURCZ, PhD. Mgr. Adriana ŠUGÁROVÁ MATEMATIKA I ZBIERKA
Matematika prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad
 Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
M6: Model Hydraulický systém dvoch zásobníkov kvapaliny s interakciou
 M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
G. Monoszová, Analytická geometria 2 - Kapitola III
 text obsahuje znenia viet, ktoré budeme dokazovat na prednáškach text je doplnený aj o množstvo poznámok, ich ciel om je dopomôct študentom k lepšiemu pochopeniu pojmov aj súvislostí medzi nimi text je
text obsahuje znenia viet, ktoré budeme dokazovat na prednáškach text je doplnený aj o množstvo poznámok, ich ciel om je dopomôct študentom k lepšiemu pochopeniu pojmov aj súvislostí medzi nimi text je
Obsah. 1.1 Reálne čísla a ich základné vlastnosti... 7 1.1.1 Komplexné čísla... 8
 Obsah 1 Číselné obory 7 1.1 Reálne čísla a ich základné vlastnosti............................ 7 1.1.1 Komplexné čísla................................... 8 1.2 Číselné množiny.......................................
Obsah 1 Číselné obory 7 1.1 Reálne čísla a ich základné vlastnosti............................ 7 1.1.1 Komplexné čísla................................... 8 1.2 Číselné množiny.......................................
Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus
 1. prednáška Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus Matematickým základom kvantovej mechaniky je teória Hilbertových
1. prednáška Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus Matematickým základom kvantovej mechaniky je teória Hilbertových
1.4 Rovnice, nerovnice a ich sústavy
 1. Rovnice, nerovnice a ich sústavy Osah Pojmy: rovnica, nerovnica, sústava rovníc, sústava nerovníc a ich riešenie, koeficient, koreň, koreňový činiteľ, diskriminant, doplnenie do štvorca, úprava na súčin,
1. Rovnice, nerovnice a ich sústavy Osah Pojmy: rovnica, nerovnica, sústava rovníc, sústava nerovníc a ich riešenie, koeficient, koreň, koreňový činiteľ, diskriminant, doplnenie do štvorca, úprava na súčin,
Numerické metódy, pravdepodobnosť a matematická štatistika. Ján BUŠA Viktor PIRČ Štefan SCHRÖTTER
 Numerické metódy, pravdepodobnosť a matematická štatistika Ján BUŠA Viktor PIRČ Štefan SCHRÖTTER Košice 2006 RECENZOVALI: Prof. RNDr. Jozef Doboš, CSc. Doc. RNDr. Vladimír Penjak, CSc. Prvé vydanie Za
Numerické metódy, pravdepodobnosť a matematická štatistika Ján BUŠA Viktor PIRČ Štefan SCHRÖTTER Košice 2006 RECENZOVALI: Prof. RNDr. Jozef Doboš, CSc. Doc. RNDr. Vladimír Penjak, CSc. Prvé vydanie Za
PageRank algoritmus. Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky
 Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky PageRank algoritmus Bakalárska práca Študijný program: Informatika Študijný odbor: 9.2.1 Informatika Školiace pracovisko: Katedra
Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky PageRank algoritmus Bakalárska práca Študijný program: Informatika Študijný odbor: 9.2.1 Informatika Školiace pracovisko: Katedra
Definícia parciálna derivácia funkcie podľa premennej x. Definícia parciálna derivácia funkcie podľa premennej y. Ak existuje limita.
 Teória prednáška č. 9 Deinícia parciálna deriácia nkcie podľa premennej Nech nkcia Ak eistje limita je deinoaná okolí bod [ ] lim. tak túto limit nazýame parciálno deriácio nkcie podľa premennej bode [
Teória prednáška č. 9 Deinícia parciálna deriácia nkcie podľa premennej Nech nkcia Ak eistje limita je deinoaná okolí bod [ ] lim. tak túto limit nazýame parciálno deriácio nkcie podľa premennej bode [
NUMERICKÁ MATEMATIKA A MATEMATICKÁ ŠTATISTIKA
 Moderné vzdelávanie pre vedomostnú spoločnosť Projekt je spolufinancovaný zo zdrojov EÚ NUMERICKÁ MATEMATIKA A MATEMATICKÁ ŠTATISTIKA Stavebná fakulta Doc.Ing. Roman Vodička, PhD. RNDr. PavolPurcz, PhD.
Moderné vzdelávanie pre vedomostnú spoločnosť Projekt je spolufinancovaný zo zdrojov EÚ NUMERICKÁ MATEMATIKA A MATEMATICKÁ ŠTATISTIKA Stavebná fakulta Doc.Ing. Roman Vodička, PhD. RNDr. PavolPurcz, PhD.
Obyčajné diferenciálne rovnice
 (ÚMV/MAN3b/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 14.3.2013 Úvod patria k najdôležitejším a najviac prepracovaným matematickým disciplínam. Nielen v minulosti, ale aj v súčastnosti predstavujú
(ÚMV/MAN3b/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 14.3.2013 Úvod patria k najdôležitejším a najviac prepracovaným matematickým disciplínam. Nielen v minulosti, ale aj v súčastnosti predstavujú
Úvod 2 Predhovor... 2 Sylaby a literatúra... 2 Označenia... 2
 Obsah Úvod Predhovor Sylaby a literatúra Označenia Euklidovské vektorové priestory 3 Skalárny súčin 3 Gram-Schmidtov ortogonalizačný proces 8 Kvadratické formy 6 Definícia a základné vlastnosti 6 Kanonický
Obsah Úvod Predhovor Sylaby a literatúra Označenia Euklidovské vektorové priestory 3 Skalárny súčin 3 Gram-Schmidtov ortogonalizačný proces 8 Kvadratické formy 6 Definícia a základné vlastnosti 6 Kanonický
Tomáš Madaras Prvočísla
 Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Numerické metódy, pravdepodobnosť a matematická štatistika
 Numerické metódy, pravdepodobnosť a matematická štatistika Ján BUŠA Viktor PIRČ Štefan SCHRÖTTER Strana 1 z 262 Košice 2006 RECENZOVALI: Prof. RNDr. Jozef Doboš, CSc. Doc. RNDr. Vladimír Penjak, CSc. Strana
Numerické metódy, pravdepodobnosť a matematická štatistika Ján BUŠA Viktor PIRČ Štefan SCHRÖTTER Strana 1 z 262 Košice 2006 RECENZOVALI: Prof. RNDr. Jozef Doboš, CSc. Doc. RNDr. Vladimír Penjak, CSc. Strana
Matematika 2. časť: Analytická geometria
 Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
6 Limita funkcie. 6.1 Myšlienka limity, interval bez bodu
 6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
Integrovanie racionálnych funkcií
 Integrovanie racionálnych funkcií Tomáš Madaras 2009-20 Z teórie funkcií už vieme, že každá racionálna funkcia (t.j. podiel dvoch polynomických funkcií) sa dá zapísať ako súčet polynomickej funkcie a funkcie
Integrovanie racionálnych funkcií Tomáš Madaras 2009-20 Z teórie funkcií už vieme, že každá racionálna funkcia (t.j. podiel dvoch polynomických funkcií) sa dá zapísať ako súčet polynomickej funkcie a funkcie
Numerické metódy Učebný text pre bakalárske štúdium
 Imrich Pokorný Numerické metódy Učebný text pre bakalárske štúdium Strana 1 z 48 1 Nepresnosť numerického riešenia úloh 4 1.1 Zdroje chýb a ich klasifikácia................... 4 1.2 Základné pojmy odhadu
Imrich Pokorný Numerické metódy Učebný text pre bakalárske štúdium Strana 1 z 48 1 Nepresnosť numerického riešenia úloh 4 1.1 Zdroje chýb a ich klasifikácia................... 4 1.2 Základné pojmy odhadu
Moderné vzdelávanie pre vedomostnú spoločnosť Projekt je spolufinancovaný zo zdrojov EÚ M A T E M A T I K A
 M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
Faculty of Mathematics, Physics and Informatics Comenius University Bratislava. NumDif
 Numerické riešenie diferenciálnych rovníc Jela Babušíková Faculty of Mathematics, Physics and Informatics Comenius University Bratislava Klasifikácia diferenciálnych rovníc: obyčajné - počiatočná a okrajová
Numerické riešenie diferenciálnych rovníc Jela Babušíková Faculty of Mathematics, Physics and Informatics Comenius University Bratislava Klasifikácia diferenciálnych rovníc: obyčajné - počiatočná a okrajová
Lineárne kódy. Ján Karabáš. Kódovanie ZS 13/14 KM FPV UMB. J. Karabáš (FPV UMB) Lineárne kódy Kodo ZS 13/14 1 / 19
 Lineárne kódy Ján Karabáš KM FPV UMB Kódovanie ZS 13/14 J. Karabáš (FPV UMB) Lineárne kódy Kodo ZS 13/14 1 / 19 Algebraické štruktúry Grupy Grupa je algebraická štruktúra G = (G;, 1, e), spolu s binárnou
Lineárne kódy Ján Karabáš KM FPV UMB Kódovanie ZS 13/14 J. Karabáš (FPV UMB) Lineárne kódy Kodo ZS 13/14 1 / 19 Algebraické štruktúry Grupy Grupa je algebraická štruktúra G = (G;, 1, e), spolu s binárnou
Technická univerzita v Košiciach. Zbierka riešených a neriešených úloh. z matematiky. pre uchádzačov o štúdium na TU v Košiciach
 Technická univerzita v Košiciach Zbierka riešených a neriešených úloh z matematiky pre uchádzačov o štúdium na TU v Košiciach Martin Bača Ján Buša Andrea Feňovčíková Zuzana Kimáková Denisa Olekšáková Štefan
Technická univerzita v Košiciach Zbierka riešených a neriešených úloh z matematiky pre uchádzačov o štúdium na TU v Košiciach Martin Bača Ján Buša Andrea Feňovčíková Zuzana Kimáková Denisa Olekšáková Štefan
Podmienenost problému a stabilita algoritmu
 Podmienenost problému a stabilita algoritmu Ing. Gabriel Okša, CSc. Matematický ústav Slovenská akadémia vied Bratislava Stavebná fakulta STU G. Okša: Podmienenost a stabilita 1/19 Obsah 1 Vektorové a
Podmienenost problému a stabilita algoritmu Ing. Gabriel Okša, CSc. Matematický ústav Slovenská akadémia vied Bratislava Stavebná fakulta STU G. Okša: Podmienenost a stabilita 1/19 Obsah 1 Vektorové a
Pevné ložiská. Voľné ložiská
 SUPPORTS D EXTREMITES DE PRECISION - SUPPORT UNIT FOR BALLSCREWS LOŽISKA PRE GULIČKOVÉ SKRUTKY A TRAPÉZOVÉ SKRUTKY Výber správnej podpory konca uličkovej skrutky či trapézovej skrutky je dôležité pre správnu
SUPPORTS D EXTREMITES DE PRECISION - SUPPORT UNIT FOR BALLSCREWS LOŽISKA PRE GULIČKOVÉ SKRUTKY A TRAPÉZOVÉ SKRUTKY Výber správnej podpory konca uličkovej skrutky či trapézovej skrutky je dôležité pre správnu
1. písomná práca z matematiky Skupina A
 1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
Chí kvadrát test dobrej zhody. Metódy riešenia úloh z pravdepodobnosti a štatistiky
 Chí kvadrát test dobrej zhody Metódy riešenia úloh z pravdepodobnosti a štatistiky www.iam.fmph.uniba.sk/institute/stehlikova Test dobrej zhody I. Chceme overiť, či naše dáta pochádzajú z konkrétneho pravdep.
Chí kvadrát test dobrej zhody Metódy riešenia úloh z pravdepodobnosti a štatistiky www.iam.fmph.uniba.sk/institute/stehlikova Test dobrej zhody I. Chceme overiť, či naše dáta pochádzajú z konkrétneho pravdep.
Numerické metódy Zbierka úloh
 Blanka Baculíková Ivan Daňo Numerické metódy Zbierka úloh Strana 1 z 37 Predhovor 3 1 Nelineárne rovnice 4 2 Sústavy lineárnych rovníc 7 3 Sústavy nelineárnych rovníc 1 4 Interpolačné polynómy 14 5 Aproximácia
Blanka Baculíková Ivan Daňo Numerické metódy Zbierka úloh Strana 1 z 37 Predhovor 3 1 Nelineárne rovnice 4 2 Sústavy lineárnych rovníc 7 3 Sústavy nelineárnych rovníc 1 4 Interpolačné polynómy 14 5 Aproximácia
3. Striedavé prúdy. Sínusoida
 . Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
. Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
Súčtové vzorce. cos (α + β) = cos α.cos β sin α.sin β cos (α β) = cos α.cos β + sin α.sin β. tg (α β) = cotg (α β) =.
 Súčtové vzorce Súčtové vzorce sú goniometrické hodnoty súčtov a rozdielov dvoch uhlov Sem patria aj goniometrické hodnoty dvojnásobného a polovičného uhla a pridám aj súčet a rozdiel goniometrických funkcií
Súčtové vzorce Súčtové vzorce sú goniometrické hodnoty súčtov a rozdielov dvoch uhlov Sem patria aj goniometrické hodnoty dvojnásobného a polovičného uhla a pridám aj súčet a rozdiel goniometrických funkcií
(IP3) (f, g) = (g, f) (symetria), (IP4) (f, f) > 0 pre f 0 (kladná definitnosť). Z podmienok (IP1) (IP4) sa ľahko dokážu rovnosti:
 Hilbertove priestory Veľké množstvo aplikácií majú lineárne normované priestory, v ktorých norma je odvodená od skalárneho (vnútorného) súčinu, podobne ako v bežnom trojrozmernom euklidovskom priestore.
Hilbertove priestory Veľké množstvo aplikácií majú lineárne normované priestory, v ktorých norma je odvodená od skalárneho (vnútorného) súčinu, podobne ako v bežnom trojrozmernom euklidovskom priestore.
Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín. Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť.
 Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť. Ktoré fyzikálne jednotky zodpovedajú sústave SI: a) Dĺžka, čas,
Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť. Ktoré fyzikálne jednotky zodpovedajú sústave SI: a) Dĺžka, čas,
PRIEMER DROTU d = 0,4-6,3 mm
 PRUŽINY PRUŽINY SKRUTNÉ PRUŽINY VIAC AKO 200 RUHOV SKRUTNÝCH PRUŽÍN PRIEMER ROTU d = 0,4-6,3 mm èíslo 3.0 22.8.2008 8:28:57 22.8.2008 8:28:58 PRUŽINY SKRUTNÉ PRUŽINY TECHNICKÉ PARAMETRE h d L S Legenda
PRUŽINY PRUŽINY SKRUTNÉ PRUŽINY VIAC AKO 200 RUHOV SKRUTNÝCH PRUŽÍN PRIEMER ROTU d = 0,4-6,3 mm èíslo 3.0 22.8.2008 8:28:57 22.8.2008 8:28:58 PRUŽINY SKRUTNÉ PRUŽINY TECHNICKÉ PARAMETRE h d L S Legenda
DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c)
 Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach Božena Mihalíková, Ivan Mojsej Strana 1 z 43 DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c) 1 Obyčajné diferenciálne rovnice 3 1.1 Úlohy
Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach Božena Mihalíková, Ivan Mojsej Strana 1 z 43 DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c) 1 Obyčajné diferenciálne rovnice 3 1.1 Úlohy
Gramatická indukcia a jej využitie
 a jej využitie KAI FMFI UK 29. Marec 2010 a jej využitie Prehľad Teória formálnych jazykov 1 Teória formálnych jazykov 2 3 a jej využitie Na počiatku bolo slovo. A slovo... a jej využitie Definícia (Slovo)
a jej využitie KAI FMFI UK 29. Marec 2010 a jej využitie Prehľad Teória formálnych jazykov 1 Teória formálnych jazykov 2 3 a jej využitie Na počiatku bolo slovo. A slovo... a jej využitie Definícia (Slovo)
Termodynamika. Doplnkové materiály k prednáškam z Fyziky I pre SjF Dušan PUDIŠ (2008)
 ermodynamika nútorná energia lynov,. veta termodynamická, Izochorický dej, Izotermický dej, Izobarický dej, diabatický dej, Práca lynu ri termodynamických rocesoch, arnotov cyklus, Entroia Dolnkové materiály
ermodynamika nútorná energia lynov,. veta termodynamická, Izochorický dej, Izotermický dej, Izobarický dej, diabatický dej, Práca lynu ri termodynamických rocesoch, arnotov cyklus, Entroia Dolnkové materiály
Matematická analýza pre fyzikov IV.
 119 Dodatok - klasické riešenia PDR 8.1. Parciálne diferenciálne rovnice Príklady parciálnych diferenciálnych rovníc: Lalpaceova rovnica u = 0 Helmholtzova rovnica u = λu n Lineárna transportná rovnica
119 Dodatok - klasické riešenia PDR 8.1. Parciálne diferenciálne rovnice Príklady parciálnych diferenciálnych rovníc: Lalpaceova rovnica u = 0 Helmholtzova rovnica u = λu n Lineárna transportná rovnica
Reálna funkcia reálnej premennej
 (ÚMV/MAN3a/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 18.10.2012 Úvod V každodennom živote, hlavne pri skúmaní prírodných javov, procesov sa stretávame so závislosťou veľkosti niektorých veličín od
(ÚMV/MAN3a/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 18.10.2012 Úvod V každodennom živote, hlavne pri skúmaní prírodných javov, procesov sa stretávame so závislosťou veľkosti niektorých veličín od
Deliteľnosť a znaky deliteľnosti
 Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
p(α 1 ) = u 1. p(α n ) = u n. Definícia (modulárna reprezentácia polynómu). Zobrazenie
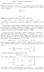 1. Rychlá Fourierová transformácia Budeme značiť teleso T a ω jeho prvok. Veta 1.1 (o interpolácií). Nech α 0, α 1,..., α n sú po dvoch rôzne prvky telesa T[x]. Potom pre každé u 0, u 1,..., u n T existuje
1. Rychlá Fourierová transformácia Budeme značiť teleso T a ω jeho prvok. Veta 1.1 (o interpolácií). Nech α 0, α 1,..., α n sú po dvoch rôzne prvky telesa T[x]. Potom pre každé u 0, u 1,..., u n T existuje
Goniometrické rovnice riešené substitúciou
 Ma-Go-10-T List 1 Goniometrické rovnice riešené substitúciou RNDr. Marián Macko U: Okrem základných goniometrických rovníc, ktorým sme sa už venovali, existujú aj zložitejšie goniometrické rovnice. Metódy
Ma-Go-10-T List 1 Goniometrické rovnice riešené substitúciou RNDr. Marián Macko U: Okrem základných goniometrických rovníc, ktorým sme sa už venovali, existujú aj zložitejšie goniometrické rovnice. Metódy
Základné vzťahy medzi hodnotami goniometrických funkcií
 Ma-Go-2-T List Základné vzťahy medzi hodnotami goniometrických funkcií RNDr. Marián Macko U: Predstav si, že ti zadám hodnotu jednej z goniometrických funkcií. Napríklad sin x = 0,6. Vedel by si určiť
Ma-Go-2-T List Základné vzťahy medzi hodnotami goniometrických funkcií RNDr. Marián Macko U: Predstav si, že ti zadám hodnotu jednej z goniometrických funkcií. Napríklad sin x = 0,6. Vedel by si určiť
Matematika 2. časť: Funkcia viac premenných Letný semester 2013/2014
 Matematika 2 časť: Funkcia viac premenných Letný semester 2013/2014 RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk
Matematika 2 časť: Funkcia viac premenných Letný semester 2013/2014 RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/27
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/27
Nelineárne optimalizačné modely a metódy
 Nelineárne optimalizačné modely a metódy Téma prednášky č. 8 Metódy transformujúce úlohu naviazaný extrém na úlohu na voľný extrém Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie
Nelineárne optimalizačné modely a metódy Téma prednášky č. 8 Metódy transformujúce úlohu naviazaný extrém na úlohu na voľný extrém Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie
1 Úvod Sylabyaliteratúra Základnéoznačenia... 3
 Obsah 1 Úvod 3 1.1 Sylabyaliteratúra.... 3 1.2 Základnéoznačenia.... 3 2 Množiny a zobrazenia 4 2.1 Dôkazy... 4 2.1.1 Základnétypydôkazov... 4 2.1.2 Matematickáindukcia... 4 2.1.3 Drobnéradyakodokazovať....
Obsah 1 Úvod 3 1.1 Sylabyaliteratúra.... 3 1.2 Základnéoznačenia.... 3 2 Množiny a zobrazenia 4 2.1 Dôkazy... 4 2.1.1 Základnétypydôkazov... 4 2.1.2 Matematickáindukcia... 4 2.1.3 Drobnéradyakodokazovať....
Fakulta matematiky, fyziky a informatiky. Univerzita Komenského. Contents I. Úvod do problematiky numeriky 2
 NUMERICKÁ MATEMATIKA ročník Fakulta matematiky, fyziky a informatiky Univerzita Komenského Contents I Úvod do problematiky numeriky II Počítačová realizácia reálnych čísel 3 III Diferenčný počet 5 IV CORDIC
NUMERICKÁ MATEMATIKA ročník Fakulta matematiky, fyziky a informatiky Univerzita Komenského Contents I Úvod do problematiky numeriky II Počítačová realizácia reálnych čísel 3 III Diferenčný počet 5 IV CORDIC
MOSTÍKOVÁ METÓDA 1.ÚLOHA: 2.OPIS MERANÉHO PREDMETU: 3.TEORETICKÝ ROZBOR: 4.SCHÉMA ZAPOJENIA:
 1.ÚLOHA: MOSTÍKOVÁ METÓDA a, Odmerajte odpory predložených rezistorou pomocou Wheastonovho mostíka. b, Odmerajte odpory predložených rezistorou pomocou Mostíka ICOMET. c, Odmerajte odpory predložených
1.ÚLOHA: MOSTÍKOVÁ METÓDA a, Odmerajte odpory predložených rezistorou pomocou Wheastonovho mostíka. b, Odmerajte odpory predložených rezistorou pomocou Mostíka ICOMET. c, Odmerajte odpory predložených
Riadenie zásobníkov kvapaliny
 Kapitola 9 Riadenie zásobníkov kvapaliny Cieľom cvičenia je zvládnuť návrh (syntézu) regulátorov výpočtovými (analytickými) metódami Naslinovou metódou a metódou umiestnenia pólov. Navrhnuté regulátory
Kapitola 9 Riadenie zásobníkov kvapaliny Cieľom cvičenia je zvládnuť návrh (syntézu) regulátorov výpočtovými (analytickými) metódami Naslinovou metódou a metódou umiestnenia pólov. Navrhnuté regulátory
Metódy numerickej matematiky I
 Úvodná prednáška Metódy numerickej matematiky I Prednášky: Doc. Mgr. Jozef Kristek, PhD. F1-207 Úvodná prednáška OBSAH 1. Úvod, sylabus, priebeh, hodnotenie 2. Zdroje a typy chýb 3. Definície chýb 4. Zaokrúhľovanie,
Úvodná prednáška Metódy numerickej matematiky I Prednášky: Doc. Mgr. Jozef Kristek, PhD. F1-207 Úvodná prednáška OBSAH 1. Úvod, sylabus, priebeh, hodnotenie 2. Zdroje a typy chýb 3. Definície chýb 4. Zaokrúhľovanie,
Vzorové riešenia 3. kola zimnej série 2014/2015
 riesky@riesky.sk Riešky matematický korešpondenčný seminár Vzorové riešenia. kola zimnej série 04/05 Príklad č. (opravovali Tete, Zuzka): Riešenie: Keďže číslo má byť deliteľné piatimi, musí končiť cifrou
riesky@riesky.sk Riešky matematický korešpondenčný seminár Vzorové riešenia. kola zimnej série 04/05 Príklad č. (opravovali Tete, Zuzka): Riešenie: Keďže číslo má byť deliteľné piatimi, musí končiť cifrou
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Diferenciálne rovnice
 Diferenciálne rovnice Juraj Tekel Katedra teoretickej fyziky a didaktiky fyziky FMFI UK Mlynska Dolina 842 48 Bratislava juraj(a)tekel(b)gmail(c)com http://fks.sk/~juro/phys_teaching.html Aktualizované
Diferenciálne rovnice Juraj Tekel Katedra teoretickej fyziky a didaktiky fyziky FMFI UK Mlynska Dolina 842 48 Bratislava juraj(a)tekel(b)gmail(c)com http://fks.sk/~juro/phys_teaching.html Aktualizované
BANACHOVE A HILBERTOVE PRIESTORY
 BANACHOVE A HILBERTOVE PRIESTORY 1. ZÁKLADNÉ POJMY Normovaným lineárnym priestorom (NLP) nazývame lineárny (= vektorový) priestor X nad telesom IK, na ktorom je daná nezáporná reálna funkcia : X IR + (norma)
BANACHOVE A HILBERTOVE PRIESTORY 1. ZÁKLADNÉ POJMY Normovaným lineárnym priestorom (NLP) nazývame lineárny (= vektorový) priestor X nad telesom IK, na ktorom je daná nezáporná reálna funkcia : X IR + (norma)
Ján Buša Štefan Schrötter
 Ján Buša Štefan Schrötter 1 KOMPLEXNÉ ČÍSLA 1 1.1 Pojem komplexného čísla Väčšine z nás je známe, že druhá mocnina ľubovoľného reálneho čísla nemôže byť záporná (ináč povedané: pre každé x R je x 0). Ako
Ján Buša Štefan Schrötter 1 KOMPLEXNÉ ČÍSLA 1 1.1 Pojem komplexného čísla Väčšine z nás je známe, že druhá mocnina ľubovoľného reálneho čísla nemôže byť záporná (ináč povedané: pre každé x R je x 0). Ako
Metoda hlavních komponent a její aplikace
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Mária Dubová Metoda hlavních komponent a její aplikace Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce:
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Mária Dubová Metoda hlavních komponent a její aplikace Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce:
Hľadanie, skúmanie a hodnotenie súvislosti medzi znakmi
 Hľadanie, skúmanie a hodnotenie súvislosti medzi znakmi Typy súvislostí javov a vecí: nepodstatné - vonkajšia súvislosť nevyplýva z vnútornej potreby (javy spoločne vznikajú, majú zhodný priebeh, alebo
Hľadanie, skúmanie a hodnotenie súvislosti medzi znakmi Typy súvislostí javov a vecí: nepodstatné - vonkajšia súvislosť nevyplýva z vnútornej potreby (javy spoločne vznikajú, majú zhodný priebeh, alebo
AerobTec Altis Micro
 AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
Spriahnute oscilatory
 Spriahnute oscilatory Juraj Tekel 1 Tema spriahnutych oscilatorov je na strednej skole vacsinou vynechana. Je vsak velmi zaujimava a velmi dolezita. Ide o situaciu, ked sa sustava sklada z viacerych telies,
Spriahnute oscilatory Juraj Tekel 1 Tema spriahnutych oscilatorov je na strednej skole vacsinou vynechana. Je vsak velmi zaujimava a velmi dolezita. Ide o situaciu, ked sa sustava sklada z viacerych telies,
Elektromagnetické pole
 Elektromagnetické pole Elektromagnetická vlna. Maxwellove rovnice v integrálnom tvare a diferenciálnom tvare. Vlnové rovnice pre E a. Vjadrenie rýchlosti elektromagnetickej vln. Vlastnosti a znázornenie
Elektromagnetické pole Elektromagnetická vlna. Maxwellove rovnice v integrálnom tvare a diferenciálnom tvare. Vlnové rovnice pre E a. Vjadrenie rýchlosti elektromagnetickej vln. Vlastnosti a znázornenie
HASLIM112V, HASLIM123V, HASLIM136V HASLIM112Z, HASLIM123Z, HASLIM136Z HASLIM112S, HASLIM123S, HASLIM136S
 PROUKTOVÝ LIST HKL SLIM č. sklad. karty / obj. číslo: HSLIM112V, HSLIM123V, HSLIM136V HSLIM112Z, HSLIM123Z, HSLIM136Z HSLIM112S, HSLIM123S, HSLIM136S fakturačný názov výrobku: HKL SLIMv 1,2kW HKL SLIMv
PROUKTOVÝ LIST HKL SLIM č. sklad. karty / obj. číslo: HSLIM112V, HSLIM123V, HSLIM136V HSLIM112Z, HSLIM123Z, HSLIM136Z HSLIM112S, HSLIM123S, HSLIM136S fakturačný názov výrobku: HKL SLIMv 1,2kW HKL SLIMv
Motivácia na zlepšenie obrazu sa používajú frekvenčné metódy a priestorové metódy.
 OBRAZOVÉ TRANSFORMÁCIE Motivácia na zlepšenie obrazu sa používajú frekvenčné metódy a priestorové metódy. Fourierova transformácia Jednorozmerný spojitý prípad Nech f(x je spojitá funkcia reálnej premennej
OBRAZOVÉ TRANSFORMÁCIE Motivácia na zlepšenie obrazu sa používajú frekvenčné metódy a priestorové metódy. Fourierova transformácia Jednorozmerný spojitý prípad Nech f(x je spojitá funkcia reálnej premennej
24. Základné spôsoby zobrazovania priestoru do roviny
 24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
množiny F G = {t1, t2,, tn} T a pre ľubovoľný valec C so základňou B1, B2,, Bn v bodoch t1, t2,, tn, takou, že pre t G - F je Bt = E, platí PF(C) = PG
 STOCHASTICKÝ PROCES Definícia stochastického procesu Definícia 1 Nech (Ω, F, P) je pravdepodobnostný priestor a nech T je podmnožina R. Pre každé t T nech X(t, ω) je náhodná premenná definovaná na pravdepodobnostnom
STOCHASTICKÝ PROCES Definícia stochastického procesu Definícia 1 Nech (Ω, F, P) je pravdepodobnostný priestor a nech T je podmnožina R. Pre každé t T nech X(t, ω) je náhodná premenná definovaná na pravdepodobnostnom
Analýza údajov. W bozóny.
 Analýza údajov W bozóny http://www.physicsmasterclasses.org/index.php 1 Identifikácia častíc https://kjende.web.cern.ch/kjende/sl/wpath_teilchenid1.htm 2 Identifikácia častíc Cvičenie 1 Na web stránke
Analýza údajov W bozóny http://www.physicsmasterclasses.org/index.php 1 Identifikácia častíc https://kjende.web.cern.ch/kjende/sl/wpath_teilchenid1.htm 2 Identifikácia častíc Cvičenie 1 Na web stránke
Harmonizované technické špecifikácie Trieda GP - CS lv EN Pevnosť v tlaku 6 N/mm² EN Prídržnosť
 Baumit Prednástrek / Vorspritzer Vyhlásenie o parametroch č.: 01-BSK- Prednástrek / Vorspritzer 1. Jedinečný identifikačný kód typu a výrobku: Baumit Prednástrek / Vorspritzer 2. Typ, číslo výrobnej dávky
Baumit Prednástrek / Vorspritzer Vyhlásenie o parametroch č.: 01-BSK- Prednástrek / Vorspritzer 1. Jedinečný identifikačný kód typu a výrobku: Baumit Prednástrek / Vorspritzer 2. Typ, číslo výrobnej dávky
UČEBNÉ TEXTY. Pracovný zošit č.2. Moderné vzdelávanie pre vedomostnú spoločnosť Elektrotechnické merania. Ing. Alžbeta Kršňáková
 Stredná priemyselná škola dopravná, Sokolská 911/94, 960 01 Zvolen Kód ITMS projektu: 26110130667 Názov projektu: Zvyšovanie flexibility absolventov v oblasti dopravy UČEBNÉ TEXTY Pracovný zošit č.2 Vzdelávacia
Stredná priemyselná škola dopravná, Sokolská 911/94, 960 01 Zvolen Kód ITMS projektu: 26110130667 Názov projektu: Zvyšovanie flexibility absolventov v oblasti dopravy UČEBNÉ TEXTY Pracovný zošit č.2 Vzdelávacia
Einsteinove rovnice. obrázkový úvod do Všeobecnej teórie relativity. Pavol Ševera. Katedra teoretickej fyziky a didaktiky fyziky
 Einsteinove rovnice obrázkový úvod do Všeobecnej teórie relativity Pavol Ševera Katedra teoretickej fyziky a didaktiky fyziky (Pseudo)historický úvod Gravitácia / Elektromagnetizmus (Pseudo)historický
Einsteinove rovnice obrázkový úvod do Všeobecnej teórie relativity Pavol Ševera Katedra teoretickej fyziky a didaktiky fyziky (Pseudo)historický úvod Gravitácia / Elektromagnetizmus (Pseudo)historický
STREDOŠKOLSKÁ MATEMATIKA
 TECHNICKÁ UNIVERZITA V KOŠICIACH FAKULTA ELEKTROTECHNIKY A INFORMATIKY KATEDRA MATEMATIKY A TEORETICKEJ INFORMATIKY STREDOŠKOLSKÁ MATEMATIKA pre študentov FEI TU v Košiciach Ján BUŠA Štefan SCHRÖTTER Košice
TECHNICKÁ UNIVERZITA V KOŠICIACH FAKULTA ELEKTROTECHNIKY A INFORMATIKY KATEDRA MATEMATIKY A TEORETICKEJ INFORMATIKY STREDOŠKOLSKÁ MATEMATIKA pre študentov FEI TU v Košiciach Ján BUŠA Štefan SCHRÖTTER Košice
HANA LAURINCOVÁ KLASICKÝ VS. NEPARAMETRICKÝ PRÍSTUP Štatistika Poistná matematika
 UNIVERZITA KOMENSKÉHO, BRATISLAVA FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA POISTNEJ MATEMATIKY A ŠTATISTIKY PARCIÁLNA A MNOHONÁSOBNÁ KORELÁCIA: KLASICKÝ VS. NEPARAMETRICKÝ PRÍSTUP (Bakalárska práca)
UNIVERZITA KOMENSKÉHO, BRATISLAVA FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA POISTNEJ MATEMATIKY A ŠTATISTIKY PARCIÁLNA A MNOHONÁSOBNÁ KORELÁCIA: KLASICKÝ VS. NEPARAMETRICKÝ PRÍSTUP (Bakalárska práca)
