ALGEBRA. Číselné množiny a operácie s nimi. Úprava algebrických výrazov
|
|
|
- Ελλάδιος Ζαΐμης
- 5 χρόνια πριν
- Προβολές:
Transcript
1 ALGEBRA Číselné množiny a operácie s nimi. Úprava algebrických výrazov Definícia Množinu považujeme za určenú, ak vieme o ľubovoľnom objekte rozhodnúť, či je alebo nie je prvkom množiny. Množinu určujeme spravidla jedným z týchto spôsobov vymenovaním vypísaním všetkých prvkov, napr. A { 4 3,}, B {a, b}, C {0} uvedením charakteristických vlastností prvkov, ktoré patria do množiny, napr. množina študentov. ročníka na FEI TU v Košiciach v roku 03 alebo množina A {x R x < }. Definícia Nech A, B sú množiny. Zápis A B označuje ich rovnosť, A B ich zjednotenie, A B ich prienik, A B ich rozdiel v danom poradí. Zápis A B znamená, že množina A je podmnožinou množiny B. Ak A B, tak množinu B A nazývame doplnok množiny A v množine B. Číselné množiny obory definujeme intuitívne na základe ich vlastností exaktné definície sú viazané na zložitý matematický aparát. Budeme používať tieto označenia N obor prirodzených čísel množina všetkých prirodzených čísel. Sú to čísla,, 3, 4, 5,... Slúžia na vyjadrenie počtu Z obor celých čísel množina všetkých celých čísel Q obor racionálnych čísel množina všetkých racionálnych čísel R obor reálnych čísel množina všetkých reálnych čísel C obor komplexných čísel množina všetkých komplexných čísel. Číselné obory sú vo vzájomnom vzťahu, ktorý môžeme zapísať takto N Z Q R C. Každé reálne číslo, ktoré nie je racionálne, nazývame iracionálnym číslom. V každom číselnom obore používame základné operácie sčítanie a násobenie. Ostatné operácie odčítanie, delenie a umocňovanie môžeme definovať pomocou sčítania a násobenia. Uvedieme vlastnosti týchto operácií k tomu potrebujeme pojem premenná. Keď chceme jedným zápisom vyjadriť viaceré konkrétne čísla konkrétne číslo je číslo, ktoré môžeme zapísať číslicami s prípadným použitím dohodnutých symbolov napr. 3,3 a tiež sin 5,, alebo keď chceme vyjadriť jediným zápisom rovnaké počtové úkony s číslami, tak používame písmená. Takéto písmená nazývame premenné, napr. x, y, z, u, v. Grécke písmeno π je zvyčajne vyčlenené na označenie Ludolfovho čísla. Ak hovoríme o premennej, takmer vždy je nevyhnutné poznať obor premennej O, čo je číselná množina, ktorej prvky premenná zastupuje. Obor reálnych čísel tvorí najdôležitejšiu číselnú množinu. Vymedzíme ju popisom základných vlastností operácií a usporiadania odporúčame premyslieť si, či sú tieto vlastnosti splnené v ostatných číselných množinách. Nech a, b, c sú ľubovoľné reálne čísla. Potom Niektorí autori zahŕňajú do množiny prirodzených čísel aj číslo 0.
2 operácie sčítania a násobenia sú uzavreté v R, t. j. a + b R, a b R platí komutatívnosť sčítania a násobenia a + b b + a a b b a platí asociatívnosť sčítania a násobenia a + b + c a + b + c a b c a b c platí distributívnosť násobenia vzhľadom k sčítaniu a b + c a b + a c existuje práve jedno číslo 0 R také, že a + 0 a existuje práve jedno číslo R, 0, také, že a a k číslu a R existuje práve jedno x R také, že a + x 0. Toto číslo x nazývame opačným číslom k číslu a a označujeme ho a ak a 0, tak existuje práve jedno číslo y také, že a y. Toto číslo nazývame prevráteným číslom k číslu a a označujeme ho zápisom /a, a alebo a. Odčítanie a delenie reálnych čísel a, b definujeme takto a b a + b, a b a b pre b 0 Každé reálne číslo je na číselnej osi zobrazené práve jedným bodom. Každý bod číselnej osi je obrazom práve jedného reálneho čísla. Veta Nech a, b, c, d R, b 0, d 0. Potom. a b c d 3. a b + c d práve vtedy, keď ad bc. ab db a d ad + bc bd 4. a b c d ac bd 5. a b c d ad bc pre c 0. Usporiadanie reálnych čísel má tieto vlastnosti trichotómia usporiadania, t. j. pre každé dve reálne čísla a, b platí práve jeden z nasledujúcich troch vzťahov a < b, a b, a > b tranzitívnosť usporiadania, t. j. ak a < b, b < c, tak a < c ak a < b, tak a + c < b + c pre každé c R ak 0 < a, 0 < b, tak 0 < ab.
3 Veta Nech a, b, c, d sú ľubovoľné reálne čísla. Potom a ak a < b a c < d, tak a + c < b + d b ak a < b a c > 0, tak ac < bc c ak a < b a c < 0, tak ac > bc d ak 0 < a < b, tak b < a e ak 0 < a < b a 0 < c < d, tak ac < bd. Zápis a b a b znamená, že a < b a > b alebo a b. Platí napr. ak a b a súčasne b a, tak a b. Premyslite si, v ktorých častiach vety môžeme znak <, resp. >, zameniť za znak, resp.. Z podmnožín množiny reálnych čísel sa najčastejšie používajú intervaly a ich zjednotenia. Definícia 3 Ohraničené intervaly s krajnými bodmi a, b, a < b sú tieto množiny a, b {x R a x b} uzavretý interval a, b {x R a < x < b} otvorený interval a, b {x R a x < b} a, b {x R a < x b}. Posledné dva intervaly nazývame polootvorené alebo polouzavreté. Dĺžka veľkosť ľubovoľného z týchto štyroch intervalov je d b a. Definícia 4 Neohraničené intervaly s krajným bodom a R sú tieto množiny, a {x R x a},, a {x R x < a} a, + {x R x a}, a, + {x R x > a}. Obor reálnych čísel R zapisujeme tiež ako interval, +. Pri symbole + často znak + vynechávame. Definícia 5 Absolútna hodnota čísla a R je číslo a definované takto a pre a 0 a a pre a < 0. Pre absolútnu hodnotu platia tieto základné vlastnosti Veta 3 Nech a, b sú ľubovoľné reálne čísla. Potom platí. a 0, pričom a 0 práve vtedy, keď a 0. a a 3. a b a b a 4. b a pre b 0 5. a b a + b a + b. b Definícia 6 Nech a je ľubovoľné reálne číslo. n-tú mocninu čísla a označujeme a n definujeme takto. ak n, tak a a. ak n N a n >, tak a n a } a {{... a} n činiteľov 3
4 3. ak n 0, a 0, tak a 0 4. ak n N, tak pre a 0 je a n a n. Veta 4 Pre každé a R, a 0 a každé n N existuje práve jedno číslo x R, x 0, také, že x n a. Definícia 7 Nech a je nezáporné reálne číslo a n prirodzené číslo. n-tú odmocninu čísla a definujeme ako nezáporné číslo x, pre ktoré platí x n a. Zapisujeme x n a. Definícia 8 n-tú odmocninu, kde n je nepárne číslo, zo záporného reálneho čísla a definujeme takto n a n a a < 0. Ak n je párne číslo, tak n-tú odmocninu zo záporného čísla v R nedefinujeme. Poznamenávame, že vyššie definovaná n-tá odmocnina reálneho čísla je v množine R uzavretá. Pripomíname, že pre ľubovoľné a R platí a a, ale 3 a3 a pre každé a R. Tieto rovnosti môžeme takto zovšeobecniť n an a pre párne n a n an a pre nepárne n. Definícia 9 Nech a > 0 je reálne číslo a m je racionálne číslo t. j. m Z a n N. Potom n definujeme tzv. racionálnu mocninu čísla a takto a m n n a m. 3 Neuvedieme presnú definíciu mocniny a r, kde a R, a > 0, pre reálny exponent r, ale uvedieme vlastnosti tejto všeobecnej mocniny. Veta 5 Nech r, s sú ľubovoľné reálne čísla. Potom platí. a r a s a r+s. a r s a rs 3. a r b r ab r 4. ar a s a r s a r 5. ar b r b 6. ak 0 < a < b a r > 0, tak a r < b r nerovnosť sa zachová, ale ak 0 < a < b a r < 0, tak a r > b r nerovnosť sa obráti 7. ak a > a r < s, tak a r < a s nerovnosť sa zachová, ale ak 0 < a < a r < s, tak a r > a s nerovnosť sa obráti 8 r pre každé r R, 0 r 0 pre každé r > 0. 4
5 Odporúčame čitateľovi, aby si premyslel otázku platnosti vzťahov 7 z vety 5 pre záporné reálne čísla a, b v prípade, keď r, s sú z množiny N, resp. Z, resp. Q. Algebrický výraz je zápis, skladajúci sa z čísel a písmen, ktoré označujú premenné. Tieto čísla a písmená sú pospájané znakmi operácií sčítanie, odčítanie, násobenie, delenie, umocnenie, odmocnenie. Obyčajne obsahujú aj zátvorky, ktoré určujú poradie naznačených operácií. Úprava výrazu V je jeho nahradenie jednoduchším výrazom V, pričom V V na definičnom obore výrazu V, ktorý zadefinujeme o chvíľu. Zjednodušenie výrazu je taký súbor úprav, po ktorých dostaneme výraz napríklad s menším počtom členov, zátvoriek, premenných dá sa povedať, že obsahuje menej znakov operácií ako obsahoval pôvodný algebrický výraz. Zvyčajne požadujeme, aby zjednodušený výraz bol napríklad v tvare súčinu alebo v tvare zlomku, ktorý sa nedá krátiť alebo aby neobsahoval odmocninu v menovateli zlomku pozri príklad. Pri úprave výrazu treba často vymedziť, pre ktoré hodnoty premenných má výraz zmysel. Určujeme pritom množinu všetkých tých hodnôt premenných, pre ktoré má výraz zmysel uvažovanú množinu nazývame definičným oborom výrazu a označujeme D. To obyčajne vedie k riešeniu rovníc alebo nerovníc. Pretože touto problematikou sa budeme zaoberať neskôr, odporúčame riešiteľovi cvičení, aby sa v prípade nejasností vrátil k tejto záležitosti po precvičení príslušných úloh z rovníc a nerovníc. Pri samotnej úprave výrazu využívame už skôr uvedené vlastnosti reálnych čísel. Pri výrazoch, ktoré obsahujú zlomky, často využívame známu vlastnosť a c b c a b pre b 0, c 0 tzv. krátenie zlomku. K tomu je potrebné upraviť výrazy v čitateli a v menovateli tak, aby obsahovali činitele s rovnakým základom v predchádzajúcom vzorci je uvažovaný rovnaký základ reprezentovaný písmenom c. To si vyžaduje istú rutinu, zbehlosť v úpravách výrazov do tvaru súčinu tieto úpravy nám pomôžu aj pri riešení rovníc a nerovníc. Uvedieme základné metódy na dosiahnutie tohto cieľa vytknutie pred zátvorku, napr. 6x 5 + 8x 3 x x 3x 3 + 4x 6 ak upravovaný výraz je kvadratický trojčlen ax + bx + c, a 0, ktorého korene nulové body sú čísla x a x pozri kapitolu o kvadratických rovniciach, tak ax + bx + c ax x x x, 4 napr. 3x 4x 4 3x x + 3 nazývaný rozklad polynómu na súčin koreňových činiteľov zovšeobecnením predchádzajúcej metódy je rozklad polynómu na súčin v prípade, ak poznáme nejaký koreň tohto polynómu to je ale v náplni učebných osnov prvého semestra na našej fakulte. Napr. číslo je koreňom polynómu y 4 + y 3 + y 4, a preto y 4 + y 3 + y 4 y + y 3 + y po združení vhodných častí výrazu vytknutie spoločného výrazu pred zátvorku, napr. 3a + az 6a z α 3aa + za β a 3a + z, 5
6 kde α v rovnosti sme združili prvý a tretí člen daného výrazu a druhý člen so štvrtým. V oboch prípadoch sme tieto združené výrazy upravili so spoločným činiteľom a v rovnosti β sme vytkli pred zátvorku tento spoločný činiteľ. často nám pomôžu nižšie uvedené vzorce, ktoré umožňujú zapísať istý typ výrazu v tvare súčinu. Pre ľubovoľné reálne čísla a a b platí a b a ba + b 5 a 3 b 3 a ba + ab + b 6 a 3 + b 3 a + ba ab + b 7 a ± ab + b a ± b 8 a 3 ± 3a b + 3ab ± b 3 a ± b 3. 9 všeobecné výrazy typu a n b n, n, môžeme zapísať v tvare súčinu, kde jeden z činiteľov je a b výraz typu a n + b n, n k, kde k N, môžeme zapísať v tvare súčinu, kde jeden z činiteľov je a s + b s, s N. Ukážky týchto úprav sú uvedené v príklade. Výrazy a + b, a 4 + b 4, a 8 + b 8 atď, sa nedajú zapísať v tvare súčinu s nejakým činiteľom typu a s + b s, s N. Zdôrazňujeme, že tieto úvahy platia v množine R neplatia v C. Príklad Vyjadrime číslo a odmocnín. + použitím čo najmenšieho počtu druhých Riešenie. a α β 3 3 β γ , 6 kde α v rovnosti sme odstránili pomocou tzv. združených výrazov odmocniny iracionality z menovateľov jednotlivých zlomkov prvý zlomok sme vynásobili vhodnou jednotkou v tvare , druhý zlomok a tretí zlomok 3 3 v rovnosti β sme upravili čitatele a menovatele zlomkov v rovnosti γ sme upravili zlomky na najmenší spoločný menovateľ. Príklad Rozložme na súčin a 5n + n + 5 b a 4 b 4 c a 6 + b 6 d a 3 3a + e x 3 + 3x 4x. Riešenie. 5n + n + 5 α [5n + + n + 5] [5n + n + 5] a 7n + 73n 3 n + n, kde v rovnosti α sme v známom vzorci 5 položili a 5n + a b n
7 b a 4 b 4 a b α a b a + b β a ba + ba + b, kde v rovnosti α sme vo vzorci 5 nahradili a s a a b s b a v rovnosti β sme použili samotný vzorec 5. c a 6 + b 6 a 3 + b 3 α a + b a 4 a b + b 4, kde v rovnosti α sme vo vzorci 7 nahradili a s a a b s b. d a 3 3a + α a 3 a a + β aa a + a γ γ a a + a δ a a a + a a +, kde v rovnosti α sme nahradili výraz 3a výrazom a a v rovnosti β sme urobili túto úpravu a 3 a aa aa a + v rovnosti γ sme vytkli pred zátvorku výraz a a upravili sme vzniknutý výraz v zátvorke v rovnosti δ sme podľa 4 upravili trojčlen a + a a a + jeho korene sú čísla a. e V tejto úlohe využijeme predchádzajúce poznatky x 3 + 3x 4x x x + 3 4x + 3 x + 3x 4 x + 3x x +. Príklad 3 Upravme v R výraz x x x x 3 tak, aby neobsahoval odmocninu. Riešenie. x x x x 3 α x x x 3 β β x 6 3 x +x, kde v rovnosti α sme podľa 8 upravili výraz x x+36 na tvar x 6 a v rovnosti β sme využili poznatok Je nevyhnutné ovládať dopĺňanie kvadratického trojčlena ax + bx + c, a 0, na úplný štvorec. Cieľom tejto úpravy je vyjadriť tento kvadratický trojčlen v tvare ax + bx + c ax m + s, 0 kde m a s sú konkrétne čísla ináč povedané upraviť výraz ax + bx + c na tvar, v ktorom premenná x vystupuje len v tvare druhej mocniny t. j. štvorca výrazu typu x mínus číslo m. Mohli by sme dokázať, že platí ax + bx + c a x b }{{} a m Ak porovnáme s 0, tak ľahko zistíme, že m b a a s + 4ac b 4a }{{} s 4ac b 4a.. Nie je potrebné zaťažovať si mozgovú kapacitu vzťahom. Stačí si uvedomiť ideu dopĺňania na štvorec pozri príklad 4 a neriešené príklady. Príklad 4 Doplňme daný kvadratický výraz na úplný štvorec a x x + 5 b 3x 6x c y 8y 4 d 5 7z. Z tejto rovnosti by sme mohli dokázať vzorec?? na výpočet koreňov kvadratickej rovnice. 7
8 Riešenie. Hlavná idea dopĺňania na štvorec spočíva vo vhodnom použití jedného zo vzorcov 8 a ± ab + b a ± b. a. Najprv vo výraze x x + 5 združíme kvadratický a lineárny člen, t. j. x x + 5 x x + 5. potom vytkneme pred zátvorky číslo, ktoré je pri x týmto krokom dostaneme v zátvorkách x x x + 5 x 6x výraz v zátvorkách upravíme tak, aby bol v tvare a ± ab + b ľavej strany vzorca 8 ak položíme a x, tak výraz ba získame úpravou 6x 3 x. Ak teraz položíme b 3, tak potrebujeme ešte získať b 3 x 6x + 5 x 3 x + 5 α x 3 x , kde v rovnosti α sme pripočítali a súčasne odčítali číslo 3 4. konečne podľa 8 dostaneme x 3 x [ x 3 3 ] jednoduchou úpravou pravej strany dostaneme x x + 5 x 3 3, čo je výraz v požadovanom tvare ax m + s, kde a, m 3 a s 3. b Zopakujeme postup z časti a tohto príkladu. Poradové čísla zodpovedajúcich krokov sme zaznamenali nad znakom 3x 6x. 3x 6x +. 3x + x x + x [ x + ] [x ] + 5. Ak porovnáme získaný výraz s 0, tak vidno, že tentoraz je a 3, m a s 5. c To bude jednoduchšie, lebo druhý krok nie je potrebný premenná je teraz y y 8y 4. y 8y 4 3. y 4 y [ x 4 4 ] 4 5. x 4 0. Pripomíname, že a, m 4 a s 0. d Koeficient pri z je vo výraze 5 7z rovný nule. V takomto prípade nemusíme dopĺňať na štvorec, lebo daný výraz je v tvare 0. Stačí si uvedomiť, že 5 7z 7 z Odtiaľ vidno, že a 7, m 0 a s 5. Je potrebné mať istú zručnosť aj v úpravách výrazov, v ktorých vystupujú zlomky. Tu sa musíme vo väčšine prípadov držať týchto hlavných zásad 8
9 ak sa nejaký zlomok vo výraze dá krátiť, tak najprv zlomok krátime a potom robíme ďalšie prípadné úpravy v prípade sčitovania alebo odčitovania zlomkov nepodceniť najmenší spoločný menovateľ zlomkov. Ukážeme to na jednoduchom prípade úprav racionálnych čísel máme upraviť číslo Ak nebudeme rešpektovať spomínané zásady, tak môžeme za spoločného menovateľa zobrať súčin menovateľov Tu by sme sa asi bez kalkulačky pomýlili. Ak si ale všimneme, že prvý zlomok môžeme po krátení upraviť na tvar 9 3, tak dostaneme To už bolo o máličko lepšie, ale ak si uvedomíme, že najmenším spoločným menovateľom je číslo 60, tak Je evidentné, že posledné úpravy boli najvhodnejšie. V predchádzajúcich dvoch prípadoch sme dostali zlomky, ktoré sa dajú krátiť hoci sme ich čitatele nevyčíslili. A teraz si predstavme, že by sme upravovali výraz s premennými a nedodržali by sme obe hlavné zásady úprav zlomkov. Dostali by sme zlomok, ktorý sa vo väčšine prípadov bude dať krátiť, ale jeho úprava bude oveľa náročnejšia. Príklad 5 Zjednodušme v R daný výraz V a určme kedy má zmysel a V x x + 5 x 8 + x + 7 x 8x + 8 b V a, b, x, y 9x y 4a 4a b 3 a 3 3b 7xy c V u d V a, x 6 u 5 3 u 7 u 4 a 9 6 x a 3a + 9a 5 3 u 8 0 u 9 u 3 x x x x 0 3a 9 3x 3a + ax r s s 3 r + r s e V r, s r r s + r r s r + r s f V x, y x y 3 + x x + y y x x + y + 3 xy 3y. y x y Riešenie. 9 x3 7 3a 5.
10 a V x α x + 5 x 9x x + 7 x 9 x 9 x + 3 x + x + 9 β x + 5x 9 + x + 7x + 9 x 9 x + 9 γ x + x + 8 x + 9 x + 3 x + x + 9 δ x 9 x + 3 x + x + 9 x + 3 x + 9x + 3 x + x + 9 x + 9 x + x + 9 x x + 9 pre x R { 3 9 9}, kde v rovnosti α sme urobili tieto úpravy podľa 5 je x 8 x 9x + 9 a na základe 8 je x 8x+8 x 9 a delenie zlomkom x+3 sme nahradili násobením zlomkom x 9 x+3 v rovnosti β sme sčítali prvé dva zlomky ich najmenší spoločný menovateľ je x 9 x+ + 9 v rovnosti γ sme upravili čitateľa prvého zlomku v rovnosti δ sme podľa 8 takto upravili čitateľa prvého zlomku x + x + 8 x + 6x + 9 x + 3 výrazy, ktorými boli jednotlivé zlomky upravené krátením sme typograficky zvýraznili rovnako budeme postupovať aj v ďalších častiach tohto príkladu. b V a, b, x, y a3 b 3 xy b pre a 0, b 0, x 0, y 0, 3 7 a 3 b xy pričom sme viacnásobne využili poznatky vety 5. c V u u 5 u 7 3 u 4 u 5 6 u u 5 x u u u 9 0 u 3 0 u 5 u 43 3 u 3 pre u > 0, pričom sme opäť použili vetu 5 a definíciu 3. d V a, x α β 3aa + 3 3a x 3 7 a 3a + 3 x a x 3a 3 3a 3ax 3 x + a a 3x ax 3 x 3x + 3x + 9 3a a 3 a 3x a x + 3x + 9 x + 3x + 9 x a pre x a, a 0, a ±3. Tu sme použili tieto úpravy v rovnosti α je a 9 a 3a + 3, ďalej 3a + 9a 3aa + 3, delenie zlomkom x a 3a +9a sme nahradili násobením prevráteným zlomkom 3aa+3 a napokon sme použili úpravu na x a súčin 9 3x 3a + ax x 3a 3 v rovnosti β sme po krátení výrazom a + 3 upravili zlomky v zátvorkách na najmenší spoločný menovateľ a 3x ax 3 a podľa 6 sme dostali x 3 7 x x 3x + 3x
11 e V r, s α r + r s + r r s r r s r + s 3 r s r s β r s s 3 γ r s r + ss s r s r s s r + s pre r > s > 0, s r, kde v rovnosti α sme sčítali prvé dva zlomky v rovnosti β sme upravili čitateľa a menovateľa vzniknutého zlomku γ v rovnosti sme krátili zlomok výrazom s a vzhľadom na to, že menovateľ druhého zlomku je v tvare r s, tak sme výraz r s na základe 5 zapísali takto r s r s r s r + s, čo nám umožní krátenie vzniknutého výrazu. f V x, y x x 3x y + 3y x y y + x x + y y x y 3 3 y x y + x y x + y 3 xx xy + y x + yx xy + y + 3 y x + y 3 x + y x + y 3 pre x 0, y 0, x y, kde sme postupne použili tieto úpravy podľa 9 je x y 3 x x 3x y + 3y x y y je zrejmé, že x x x x podľa 7 je x x + y y x 3 + y 3 x + yx xy + y čitateľ prvého zlomku má po úprave tvar 3x x 3x y + 3y x a taktiež ho môžeme zapísať takto v tvare súčinu 3 xx xy + y keďže čitateľ 3 xy 3y druhého zlomku môžeme zapísať v tomto tvare súčinu 3 xy 3y 3 y x y, tak na základe 5 zapíšeme jeho menovateľa takto x y x y x y x+ y, čo nám umožní zlomok krátiť výrazom x y. Na záver tohto oddielu uvádzame väčšie množstvo neriešených úloh na úpravy výrazov. Odporúčame vám, aby ste sa pokúsili vyriešiť čo najviac úloh. Nedajte sa odradiť prípadným neúspechom. Na vlastných chybách sa človek najlepšie učí. Môže vám to pomôcť v nadobudnutí zbehlosti v riešení tých úloh, ktoré vás očakávajú.
12 Úlohy. Upravte zjednodušte daný číselný výraz a [8] b [ 3/9] c, [ 4/5,64] d [ 35/7] 3 e 0, [ 9/5,8] f [ 6/9] g h 0,6 0, [ 76/75,033] 3 4 i [4] [] i Rozložte v R na súčin [/45] a x 3 x x + [x x ] b x 3 x + 4x 4 [x + 4x ] c x 3 + 3x + 3x + [x + 3 x + x + ] d x 3 9x + 7x 7 [x 3 3 x 3x 6x + 9] e x 3 6x + x 8 [x 3 x x ] f 6n + 7 n 3 [35n + n + 4] g x + y 4 x y 4 [8xyx + y h a 4 + a 3 + 6a + 5a + 5 [a + 5a + a + ] i x x [xx + 7] j 7b 3 54b + 36b 8 [3b 3 ] k 7b 3 3b + b 8. [3b 9b + 5b + 4] 3. Doplňte daný výraz na štvorec a x x + [x + ]
13 b x + 4x 7 [x + ] c x 5x + [x 5/ /4] d x + 0x + e 6y y [x + 5 3] [ y 3 + 9] f 8 7a [ 7a + 8] g 3x 5x + [3x 5/6 /] h z z [ z ] i x x. [x 3 0] 4. Upravte zjednodušte daný výraz a b c x x 4 x + 3x x x 6x + 9 x x+3 4 4x x +3x [/3x ] 5x [/53 x] 3 x [xx /4x ] d x x x + x [x /x ] xx x e x [x 4x/x xx 4/x ] f xx + 3 x x + [ x + 4x + 3/x + x + 3x + /x + ] g x4 x x x 4 x [8x/x 4 ] h xx + 4 x x x + 4 [8x/x + 4 ] i x x x x 4 [ x/x 3 ] j 3x x + x 3 4x + 4x + 4. [x x + 3/x + 3 x 3 + 3x /x + 3 ] 5. Zjednodušte dané výrazy a určte ich definičné obory a a 3 9b4 5c 3b 3 4c 5c 3 3a 3a [a /9b 5 a 0, b 0, c 0] b x + ya+ u v u v a+ x ya+, kde a N [x y u v, x ±y] a x y a+ u v c ax+3y b 4x 5y a 5x y b 3x+y a4x+5y b x 4y a 8x+y b x+y pre a > 0, b > 0 [a x+y ] a b 4 3 a 3 b 3 d [b 6 /c 5 d a 0, b 0, c 0, d 0] c 3 d c d 3
14 e a + b 3 ab b a ab [a/ab a 0, b 0, ab ±] f r + s r s r s r + s r + s [ r/s r ±s, s 0] r s g h i j + b a a 4 b 4 a b a b + a b [a + b/a b a 0, b 0, a b] z + z z z [/z z R {0 }] + 6ac a 3 8c 3 a c a 3 8c 3 a + ca + 4c a a a a + [ + a c a c, a c ] a 0,5a 4 a 3 + 4a 8 [a a + 4 a / {0 ±}] x k x + x + + x + x + x + x + x + x x [/x 3 x 0] x + x l a + a ,5a a + + [/a a / {0, ±}] a a a x + a x a x a x m b y + b y b y b y n [ a a 6 9 a + 3 a ] a + 3 a x b y o x + x + 5 x x 8 + x + 7 x 8x + 8 p + 4y y 8y 3 + q b + a 4a b a b 3 + ab 3a b r 8 3x + 9 3x x + x 3 s + a x + b y + [b y /a x x 0, y 0, a > 0, b > 0, a,b ] 4a 8 a + a [ a / {0 ±3}] 4 a 9 x + 3 [ x / { 3 ±9}] x 8 y 4y + 4y y + y [/y y ±0,5] a3 b + a b + ab 3 4a b a b 3x x x + 3x [a b/a + b a 0, b 0, a ±b, b 3a] [3/x x / {0 ±3}] a 4 + a a a + a a [a/ a / {0 ±}] a 3 4a 4
15 t a 5 + a u v [ 3 + a + 4a 3 4a + a a 8a 4a + a + 3 a + a [0, a / {0 ±0,5}] ] [ ] x x + x + x + 3 x3 + [x /x + x ±] x 3 a x 4 a + ax 3 a x a + 4 ax 4 ax [ 4 ax a 0, b 0, a 0] w a,5 b,5 a b a 0,5 + b 0,5 0,5 [0 a 0 b > 0 b 0 a > 0] b a a b x a + b + a a b b a + b + b a b a [a a ±b] y [ ab aba + ab ] ab b [a ab > 0, a b] a b z A m + n m + n + m + n mn n m nm x ax a + x + x ax a B 3x m nm + n [ m n m, n > 0, n m] 3x + x 3 + x [/a a 0, x, 3, a] 9x 9x 9x [/3x + x ±/3] 3x + C x 4 x3 + x x + 4 x x + 4 x + [ x x > 0] [ ] x [ ] D + x + x + x + x + [/x + x 0 {}] x E a b 3 a 3 b a + b 3 a + 3 b [ 3 ab b ±a] F a b a3 b 3 [ ab/ a + b a 0, b 0, a b] a b a b G x x x + x [/x pre x > a x / x pre x < ] 4 x3 4 x H x + + x / [/ + x x x x x > 0, x ] x I + + x x x [ x x 0, x < ] x 5
16 J s s + K s 3 s 3p r + 3pr 4 7p 3 r 3 + s + 9p + 3pr + r + s [ s s 0 < s < ] s r [r 3p, 3p + r ±] r 3 7p 3 L a + b 4b a b b + 3 a a + 9b + 6 ab a + b [/ab a > 0, b > 0, a b.] 6
Matematika Funkcia viac premenných, Parciálne derivácie
 Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
STREDOŠKOLSKÁ MATEMATIKA
 TECHNICKÁ UNIVERZITA V KOŠICIACH FAKULTA ELEKTROTECHNIKY A INFORMATIKY KATEDRA MATEMATIKY A TEORETICKEJ INFORMATIKY STREDOŠKOLSKÁ MATEMATIKA pre študentov FEI TU v Košiciach Ján BUŠA Štefan SCHRÖTTER Košice
TECHNICKÁ UNIVERZITA V KOŠICIACH FAKULTA ELEKTROTECHNIKY A INFORMATIKY KATEDRA MATEMATIKY A TEORETICKEJ INFORMATIKY STREDOŠKOLSKÁ MATEMATIKA pre študentov FEI TU v Košiciach Ján BUŠA Štefan SCHRÖTTER Košice
Výrazy a ich úpravy. -17x 6 : -17 koeficient; x premenná; 6 exponent premennej x. 23xy 3 z 5 = 23x 1 y 3 z 5 : 23 koeficient; x; y; z premenné;
 Výrazy a ich úpravy Počtový výraz je matematický zápis, ktorým vyjadrujeme počtové operácie s číslami a poradie v akom majú byť prevedené. Napr.: ( (5 1,76)+5):0,4. Počtové výrazy sa pomenovávajú podľa
Výrazy a ich úpravy Počtový výraz je matematický zápis, ktorým vyjadrujeme počtové operácie s číslami a poradie v akom majú byť prevedené. Napr.: ( (5 1,76)+5):0,4. Počtové výrazy sa pomenovávajú podľa
Cvičenie č. 4,5 Limita funkcie
 Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
6 Limita funkcie. 6.1 Myšlienka limity, interval bez bodu
 6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
7. FUNKCIE POJEM FUNKCIE
 7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
Integrovanie racionálnych funkcií
 Integrovanie racionálnych funkcií Tomáš Madaras 2009-20 Z teórie funkcií už vieme, že každá racionálna funkcia (t.j. podiel dvoch polynomických funkcií) sa dá zapísať ako súčet polynomickej funkcie a funkcie
Integrovanie racionálnych funkcií Tomáš Madaras 2009-20 Z teórie funkcií už vieme, že každá racionálna funkcia (t.j. podiel dvoch polynomických funkcií) sa dá zapísať ako súčet polynomickej funkcie a funkcie
Start. Vstup r. O = 2*π*r S = π*r*r. Vystup O, S. Stop. Start. Vstup P, C V = P*C*1,19. Vystup V. Stop
 1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
Goniometrické rovnice a nerovnice. Základné goniometrické rovnice
 Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
PRÍPRAVNÝ KURZ ZO STREDOŠKOLSKEJ MATEMATIKY
 Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ PRÍPRAVNÝ KURZ ZO STREDOŠKOLSKEJ MATEMATIKY Strojnícka fakulta Andrea Feňovčíková Gabriela Ižaríková aaaa aaaa Táto
Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ PRÍPRAVNÝ KURZ ZO STREDOŠKOLSKEJ MATEMATIKY Strojnícka fakulta Andrea Feňovčíková Gabriela Ižaríková aaaa aaaa Táto
Ján Buša Štefan Schrötter
 Ján Buša Štefan Schrötter 1 KOMPLEXNÉ ČÍSLA 1 1.1 Pojem komplexného čísla Väčšine z nás je známe, že druhá mocnina ľubovoľného reálneho čísla nemôže byť záporná (ináč povedané: pre každé x R je x 0). Ako
Ján Buša Štefan Schrötter 1 KOMPLEXNÉ ČÍSLA 1 1.1 Pojem komplexného čísla Väčšine z nás je známe, že druhá mocnina ľubovoľného reálneho čísla nemôže byť záporná (ináč povedané: pre každé x R je x 0). Ako
Technická univerzita v Košiciach. Zbierka riešených a neriešených úloh. z matematiky. pre uchádzačov o štúdium na TU v Košiciach
 Technická univerzita v Košiciach Zbierka riešených a neriešených úloh z matematiky pre uchádzačov o štúdium na TU v Košiciach Martin Bača Ján Buša Andrea Feňovčíková Zuzana Kimáková Denisa Olekšáková Štefan
Technická univerzita v Košiciach Zbierka riešených a neriešených úloh z matematiky pre uchádzačov o štúdium na TU v Košiciach Martin Bača Ján Buša Andrea Feňovčíková Zuzana Kimáková Denisa Olekšáková Štefan
Komplexné čísla, Diskrétna Fourierova transformácia 1
 Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
1. Limita, spojitost a diferenciálny počet funkcie jednej premennej
 . Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
. Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
Matematika prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad
 Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
Tomáš Madaras Prvočísla
 Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Moderné vzdelávanie pre vedomostnú spoločnosť Projekt je spolufinancovaný zo zdrojov EÚ M A T E M A T I K A
 M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
Ekvačná a kvantifikačná logika
 a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
1. písomná práca z matematiky Skupina A
 1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
Obvod a obsah štvoruholníka
 Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Funkcie - základné pojmy
 Funkcie - základné pojmy DEFINÍCIA FUNKCIE Nech A, B sú dve neprázdne číselné množiny. Ak každému prvku x A je priradený najviac jeden prvok y B, tak hovoríme, že je daná funkcia z množiny A do množiny
Funkcie - základné pojmy DEFINÍCIA FUNKCIE Nech A, B sú dve neprázdne číselné množiny. Ak každému prvku x A je priradený najviac jeden prvok y B, tak hovoríme, že je daná funkcia z množiny A do množiny
TREDNÁ ODBORNÁ ŠKOLA STRÁŽSKE PRACOVNÝ ZOŠIT. k predmetu Matematika pre
 TREDNÁ ODBORNÁ ŠKOLA STRÁŽSKE PRACOVNÝ ZOŠIT k predmetu Matematika pre 2. ročník SOŠ v Strážskom, študijný odbor 3760 6 00 prevádzka a ekonomika dopravy Operačný program: Vzdelávanie Programové obdobie:
TREDNÁ ODBORNÁ ŠKOLA STRÁŽSKE PRACOVNÝ ZOŠIT k predmetu Matematika pre 2. ročník SOŠ v Strážskom, študijný odbor 3760 6 00 prevádzka a ekonomika dopravy Operačný program: Vzdelávanie Programové obdobie:
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
3. prednáška. Komplexné čísla
 3. predáška Komplexé čísla Úvodé pozámky Vieme, že existujú také kvadratické rovice, ktoré emajú riešeie v obore reálych čísel. Študujme kvadratickú rovicu x x + 5 = 0 Použitím štadardej formule pre výpočet
3. predáška Komplexé čísla Úvodé pozámky Vieme, že existujú také kvadratické rovice, ktoré emajú riešeie v obore reálych čísel. Študujme kvadratickú rovicu x x + 5 = 0 Použitím štadardej formule pre výpočet
1. Komplexné čísla. Doteraz ste pracovali s číslami, ktoré pochádzali z nasledovných množín:
 1. Komplexné čísla Po preštudovaní danej kapitoly by ste mali byť shopní: poznať použitie a význam komplexnýh čísel v elektrikýh obvodoh rozumieť pojmom reálna a imaginárna časť, imaginárna jednotka, veľkosť,
1. Komplexné čísla Po preštudovaní danej kapitoly by ste mali byť shopní: poznať použitie a význam komplexnýh čísel v elektrikýh obvodoh rozumieť pojmom reálna a imaginárna časť, imaginárna jednotka, veľkosť,
Deliteľnosť a znaky deliteľnosti
 Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Polynómy. Hornerova schéma. Algebrické rovnice
 Polynómy. Hornerova schéma. Algebrické rovnice Teoretické základy Definícia 1 Nech (koeficienty) a 0, a 1,..., a n sú komplexné čísla a nech n je nezáporné celé číslo. Výraz P n (x) = a n x n + a n 1 x
Polynómy. Hornerova schéma. Algebrické rovnice Teoretické základy Definícia 1 Nech (koeficienty) a 0, a 1,..., a n sú komplexné čísla a nech n je nezáporné celé číslo. Výraz P n (x) = a n x n + a n 1 x
Základné vzťahy medzi hodnotami goniometrických funkcií
 Ma-Go-2-T List Základné vzťahy medzi hodnotami goniometrických funkcií RNDr. Marián Macko U: Predstav si, že ti zadám hodnotu jednej z goniometrických funkcií. Napríklad sin x = 0,6. Vedel by si určiť
Ma-Go-2-T List Základné vzťahy medzi hodnotami goniometrických funkcií RNDr. Marián Macko U: Predstav si, že ti zadám hodnotu jednej z goniometrických funkcií. Napríklad sin x = 0,6. Vedel by si určiť
Motivácia Denícia determinantu Výpo et determinantov Determinant sú inu matíc Vyuºitie determinantov. Determinanty. 14. decembra 2010.
 14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
1.4 Rovnice, nerovnice a ich sústavy
 1. Rovnice, nerovnice a ich sústavy Osah Pojmy: rovnica, nerovnica, sústava rovníc, sústava nerovníc a ich riešenie, koeficient, koreň, koreňový činiteľ, diskriminant, doplnenie do štvorca, úprava na súčin,
1. Rovnice, nerovnice a ich sústavy Osah Pojmy: rovnica, nerovnica, sústava rovníc, sústava nerovníc a ich riešenie, koeficient, koreň, koreňový činiteľ, diskriminant, doplnenie do štvorca, úprava na súčin,
Matematika 2. časť: Analytická geometria
 Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti
 4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti Výroková funkcia (forma) ϕ ( x) je formálny výraz (formula), ktorý obsahuje znak x, pričom x berieme z nejakej množiny M. Ak za x zvolíme
4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti Výroková funkcia (forma) ϕ ( x) je formálny výraz (formula), ktorý obsahuje znak x, pričom x berieme z nejakej množiny M. Ak za x zvolíme
FUNKCIE. Funkcia základné pojmy. Graf funkcie
 FUNKCIE Funkcia základné pojm. Graf funkcie V prai sa často stretávame so skúmaním závislosti veľkosti niektorých veličín od veľkosti iných veličín, napríklad dĺžka kružnice l závisí od jej priemeru d
FUNKCIE Funkcia základné pojm. Graf funkcie V prai sa často stretávame so skúmaním závislosti veľkosti niektorých veličín od veľkosti iných veličín, napríklad dĺžka kružnice l závisí od jej priemeru d
Obsah. 1.1 Reálne čísla a ich základné vlastnosti... 7 1.1.1 Komplexné čísla... 8
 Obsah 1 Číselné obory 7 1.1 Reálne čísla a ich základné vlastnosti............................ 7 1.1.1 Komplexné čísla................................... 8 1.2 Číselné množiny.......................................
Obsah 1 Číselné obory 7 1.1 Reálne čísla a ich základné vlastnosti............................ 7 1.1.1 Komplexné čísla................................... 8 1.2 Číselné množiny.......................................
Úvod do lineárnej algebry. Monika Molnárová Prednášky
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
MATEMATICKÁ ANALÝZA 1
 UNIVERZITA PAVLA JOZEFA ŠAFÁRIKA V KOŠICIACH Prírodovedecká fakulta Ústav matematických vied Božena Mihalíková, Ján Ohriska MATEMATICKÁ ANALÝZA Vysokoškolský učebný text Košice, 202 202 doc. RNDr. Božena
UNIVERZITA PAVLA JOZEFA ŠAFÁRIKA V KOŠICIACH Prírodovedecká fakulta Ústav matematických vied Božena Mihalíková, Ján Ohriska MATEMATICKÁ ANALÝZA Vysokoškolský učebný text Košice, 202 202 doc. RNDr. Božena
Definícia parciálna derivácia funkcie podľa premennej x. Definícia parciálna derivácia funkcie podľa premennej y. Ak existuje limita.
 Teória prednáška č. 9 Deinícia parciálna deriácia nkcie podľa premennej Nech nkcia Ak eistje limita je deinoaná okolí bod [ ] lim. tak túto limit nazýame parciálno deriácio nkcie podľa premennej bode [
Teória prednáška č. 9 Deinícia parciálna deriácia nkcie podľa premennej Nech nkcia Ak eistje limita je deinoaná okolí bod [ ] lim. tak túto limit nazýame parciálno deriácio nkcie podľa premennej bode [
Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej transformácie,
 Kapitola Riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie, keď charakteritická rovnica má rôzne
Kapitola Riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie, keď charakteritická rovnica má rôzne
Príklady na precvičovanie Fourierove rady
 Príklady na precvičovanie Fourierove rady Ďalším významným typom funkcionálnych radov sú trigonometrické rady, pri ktorých sú jednotlivé členy trigonometrickými funkciami. Konkrétne, jedná sa o rady tvaru
Príklady na precvičovanie Fourierove rady Ďalším významným typom funkcionálnych radov sú trigonometrické rady, pri ktorých sú jednotlivé členy trigonometrickými funkciami. Konkrétne, jedná sa o rady tvaru
Číslo a číslica. Pojem čísla je jedným zo základných pojmov matematiky. Číslo je abstraktná entita (fil. niečo existujúce) používaná na opis množstva.
 Číslo a číslica Pojem čísla je jedným zo základných pojmov matematiky. Číslo je abstraktná entita (fil. niečo existujúce) používaná na opis množstva. Číslica (cifra) je grafický znak, pomocou ktorého zapisujeme
Číslo a číslica Pojem čísla je jedným zo základných pojmov matematiky. Číslo je abstraktná entita (fil. niečo existujúce) používaná na opis množstva. Číslica (cifra) je grafický znak, pomocou ktorého zapisujeme
FUNKCIE N REÁLNYCH PREMENNÝCH
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE FUNKCIE N REÁLNYCH PREMENNÝCH RNDr. Kristína Rostás, PhD. PREDMET: Matematická analýza ) 2010/2011 1. DEFINÍCIA REÁLNEJ FUNKCIE
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE FUNKCIE N REÁLNYCH PREMENNÝCH RNDr. Kristína Rostás, PhD. PREDMET: Matematická analýza ) 2010/2011 1. DEFINÍCIA REÁLNEJ FUNKCIE
1 Polynómy a racionálne funkcie Základy Polynómy Cvičenia Racionálne funkcie... 17
 Obsah 1 Polynómy a racionálne funkcie 3 11 Základy 3 1 Polynómy 7 11 Cvičenia 13 13 Racionálne funkcie 17 131 Cvičenia 19 Lineárna algebra 3 1 Matice 3 11 Matice - základné vlastnosti 3 1 Cvičenia 6 Sústavy
Obsah 1 Polynómy a racionálne funkcie 3 11 Základy 3 1 Polynómy 7 11 Cvičenia 13 13 Racionálne funkcie 17 131 Cvičenia 19 Lineárna algebra 3 1 Matice 3 11 Matice - základné vlastnosti 3 1 Cvičenia 6 Sústavy
Goniometrické nerovnice
 Ma-Go--T List Goniometrické nerovnice RNDr. Marián Macko U: Problematiku, ktorej sa budeme venovať, začneme úlohou. Máme určiť definičný obor funkcie f zadanej predpisom = sin. Máš predstavu, s čím táto
Ma-Go--T List Goniometrické nerovnice RNDr. Marián Macko U: Problematiku, ktorej sa budeme venovať, začneme úlohou. Máme určiť definičný obor funkcie f zadanej predpisom = sin. Máš predstavu, s čím táto
Súčtové vzorce. cos (α + β) = cos α.cos β sin α.sin β cos (α β) = cos α.cos β + sin α.sin β. tg (α β) = cotg (α β) =.
 Súčtové vzorce Súčtové vzorce sú goniometrické hodnoty súčtov a rozdielov dvoch uhlov Sem patria aj goniometrické hodnoty dvojnásobného a polovičného uhla a pridám aj súčet a rozdiel goniometrických funkcií
Súčtové vzorce Súčtové vzorce sú goniometrické hodnoty súčtov a rozdielov dvoch uhlov Sem patria aj goniometrické hodnoty dvojnásobného a polovičného uhla a pridám aj súčet a rozdiel goniometrických funkcií
24. Základné spôsoby zobrazovania priestoru do roviny
 24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Logaritmus operácie s logaritmami, dekadický a prirodzený logaritmus
 KrAv11-T List 1 Logaritmus operácie s logaritmami, dekadický a prirodzený logaritmus RNDr. Jana Krajčiová, PhD. U: Najprv si zopakujme, ako znie definícia logaritmu. Ž: Ja si pamätám, že logaritmus súvisí
KrAv11-T List 1 Logaritmus operácie s logaritmami, dekadický a prirodzený logaritmus RNDr. Jana Krajčiová, PhD. U: Najprv si zopakujme, ako znie definícia logaritmu. Ž: Ja si pamätám, že logaritmus súvisí
Goniometrické rovnice riešené substitúciou
 Ma-Go-10-T List 1 Goniometrické rovnice riešené substitúciou RNDr. Marián Macko U: Okrem základných goniometrických rovníc, ktorým sme sa už venovali, existujú aj zložitejšie goniometrické rovnice. Metódy
Ma-Go-10-T List 1 Goniometrické rovnice riešené substitúciou RNDr. Marián Macko U: Okrem základných goniometrických rovníc, ktorým sme sa už venovali, existujú aj zložitejšie goniometrické rovnice. Metódy
Derivácia funkcie. Pravidlá derivovania výrazov obsahujúcich operácie. Derivácie elementárnych funkcií
 Derivácia funkcie Derivácia funkcie je jeden z najužitočnejších nástrojov, ktoré používame v matematike a jej aplikáciách v ďalších odboroch. Stručne zhrnieme základné informácie o deriváciách. Podrobnejšie
Derivácia funkcie Derivácia funkcie je jeden z najužitočnejších nástrojov, ktoré používame v matematike a jej aplikáciách v ďalších odboroch. Stručne zhrnieme základné informácie o deriváciách. Podrobnejšie
Prirodzené čísla. Kardinálne čísla
 Prirodzené čísla Doteraz sme sa vždy uspokojili s tým, že sme pod množinou prirodzených čísel rozumeli množinu N = { 1, 2,3, 4,5, 6, 7,8,9,10,11,12, } Túto množinu sme chápali intuitívne a presne sme ju
Prirodzené čísla Doteraz sme sa vždy uspokojili s tým, že sme pod množinou prirodzených čísel rozumeli množinu N = { 1, 2,3, 4,5, 6, 7,8,9,10,11,12, } Túto množinu sme chápali intuitívne a presne sme ju
Reálna funkcia reálnej premennej
 (ÚMV/MAN3a/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 18.10.2012 Úvod V každodennom živote, hlavne pri skúmaní prírodných javov, procesov sa stretávame so závislosťou veľkosti niektorých veličín od
(ÚMV/MAN3a/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 18.10.2012 Úvod V každodennom živote, hlavne pri skúmaní prírodných javov, procesov sa stretávame so závislosťou veľkosti niektorých veličín od
x x x2 n
 Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus
 1. prednáška Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus Matematickým základom kvantovej mechaniky je teória Hilbertových
1. prednáška Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus Matematickým základom kvantovej mechaniky je teória Hilbertových
PREHĽAD ZÁKLADNÝCH VZORCOV A VZŤAHOV ZO STREDOŠKOLSKEJ MATEMATIKY. Pomôcka pre prípravný kurz
 KATEDRA APLIKOVANEJ MATEMATIKY A INFORMATIKY STROJNÍCKA FAKULTA TU KOŠICE PREHĽAD ZÁKLADNÝCH VZORCOV A VZŤAHOV ZO STREDOŠKOLSKEJ MATEMATIKY Pomôcka pre prípravný kurz 8 ZÁKLADNÉ ALGEBRAICKÉ VZORCE ) (a±b)
KATEDRA APLIKOVANEJ MATEMATIKY A INFORMATIKY STROJNÍCKA FAKULTA TU KOŠICE PREHĽAD ZÁKLADNÝCH VZORCOV A VZŤAHOV ZO STREDOŠKOLSKEJ MATEMATIKY Pomôcka pre prípravný kurz 8 ZÁKLADNÉ ALGEBRAICKÉ VZORCE ) (a±b)
Funkcie komplexnej premennej
 (prezentácia k prednáške FKP/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prednáška 1 16. februára 2016 Podmienky Obsah nepovinná účast (!prelínanie prednášok a cvičení!)
(prezentácia k prednáške FKP/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prednáška 1 16. februára 2016 Podmienky Obsah nepovinná účast (!prelínanie prednášok a cvičení!)
TECHNICKÁ UNIVERZITA V KOŠICIACH STROJNÍCKA FAKULTA MATEMATIKA 1. Funkcia jednej premennej a jej diferenciálny počet
 TECHNICKÁ UNIVERZITA V KOŠICIACH STROJNÍCKA FAKULTA MATEMATIKA časťa Funkcia jednej premennej a jej diferenciáln počet Dušan Knežo, Miriam Andrejiová, Zuzana Kimáková 200 RECENZOVALI: prof. RNDr. Jozef
TECHNICKÁ UNIVERZITA V KOŠICIACH STROJNÍCKA FAKULTA MATEMATIKA časťa Funkcia jednej premennej a jej diferenciáln počet Dušan Knežo, Miriam Andrejiová, Zuzana Kimáková 200 RECENZOVALI: prof. RNDr. Jozef
Gymnázium v Košiciach, Opatovská 7 MATEMATIKA
 Gymnázium v Košiciach, Opatovská 7 MATEMATIKA ŠTÁTNY PEDAGOGICKÝ ÚSTAV, PLUHOVÁ 8, 80 00 BRATISLAVA VZDELÁVACÍ ŠTANDARD S EXEMPLIFIKAČNÝMI ÚLOHAMI Z MATEMATIKY PRE GYMNÁZIUM (štvorročné štúdium) Vypracoval:
Gymnázium v Košiciach, Opatovská 7 MATEMATIKA ŠTÁTNY PEDAGOGICKÝ ÚSTAV, PLUHOVÁ 8, 80 00 BRATISLAVA VZDELÁVACÍ ŠTANDARD S EXEMPLIFIKAČNÝMI ÚLOHAMI Z MATEMATIKY PRE GYMNÁZIUM (štvorročné štúdium) Vypracoval:
2. prednáška. Teória množín I. množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin
 2. prednáška Teória množín I množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin Verzia: 27. 9. 2009 Priesvtika: 1 Definícia množiny Koncepcia množiny patrí medzi
2. prednáška Teória množín I množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin Verzia: 27. 9. 2009 Priesvtika: 1 Definícia množiny Koncepcia množiny patrí medzi
XVIII. ročník BRKOS 2011/2012. Pomocný text. Kde by bola matematika bez čísel? Čísla predstavujú jednu z prvých abstrakcií, ktorú
 Pomocný text Číselné obory Číselné obory Kde by bola matematika bez čísel? Čísla predstavujú jednu z prvých abstrakcií, ktorú ľudia začali vnímať. Abstrakcia spočívala v tom, že množstvo, ktoré sa snažili
Pomocný text Číselné obory Číselné obory Kde by bola matematika bez čísel? Čísla predstavujú jednu z prvých abstrakcií, ktorú ľudia začali vnímať. Abstrakcia spočívala v tom, že množstvo, ktoré sa snažili
M6: Model Hydraulický systém dvoch zásobníkov kvapaliny s interakciou
 M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
Gramatická indukcia a jej využitie
 a jej využitie KAI FMFI UK 29. Marec 2010 a jej využitie Prehľad Teória formálnych jazykov 1 Teória formálnych jazykov 2 3 a jej využitie Na počiatku bolo slovo. A slovo... a jej využitie Definícia (Slovo)
a jej využitie KAI FMFI UK 29. Marec 2010 a jej využitie Prehľad Teória formálnych jazykov 1 Teória formálnych jazykov 2 3 a jej využitie Na počiatku bolo slovo. A slovo... a jej využitie Definícia (Slovo)
4 Reálna funkcia reálnej premennej a jej vlastnosti
 Reálna unkcia reálnej premennej a jej vlastnosti Táto kapitola je venovaná štúdiu reálnej unkcie jednej reálnej premennej. Pojem unkcie patrí medzi základné pojmy v matematike. Je to vlastne matematický
Reálna unkcia reálnej premennej a jej vlastnosti Táto kapitola je venovaná štúdiu reálnej unkcie jednej reálnej premennej. Pojem unkcie patrí medzi základné pojmy v matematike. Je to vlastne matematický
VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR. Michal Zajac. 3 T b 1 = T b 2 = = = 2b
 VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR Michal Zajac Vlastné čísla a vlastné vektory Pripomeňme najprv, že lineárny operátor T : L L je vzhl adom na bázu B = {b 1, b 2,, b n } lineárneho priestoru L určený
VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR Michal Zajac Vlastné čísla a vlastné vektory Pripomeňme najprv, že lineárny operátor T : L L je vzhl adom na bázu B = {b 1, b 2,, b n } lineárneho priestoru L určený
JKTc01-T List 1. Číselné množiny. Mgr. Jana Králiková
 JKTc01-T List 1 Číselné množiny Mgr. Jana Králiková U: Čo si predstavuješ pod pojmom množina? Ž: Skupinu nejakých vecí. U: Presnejšie by sa dalo povedať, že množina je skupina (súbor, súhrn) navzájom rôznych
JKTc01-T List 1 Číselné množiny Mgr. Jana Králiková U: Čo si predstavuješ pod pojmom množina? Ž: Skupinu nejakých vecí. U: Presnejšie by sa dalo povedať, že množina je skupina (súbor, súhrn) navzájom rôznych
Matematika 2. časť: Funkcia viac premenných Letný semester 2013/2014
 Matematika 2 časť: Funkcia viac premenných Letný semester 2013/2014 RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk
Matematika 2 časť: Funkcia viac premenných Letný semester 2013/2014 RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk
Obyčajné diferenciálne rovnice
 (ÚMV/MAN3b/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 14.3.2013 Úvod patria k najdôležitejším a najviac prepracovaným matematickým disciplínam. Nielen v minulosti, ale aj v súčastnosti predstavujú
(ÚMV/MAN3b/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 14.3.2013 Úvod patria k najdôležitejším a najviac prepracovaným matematickým disciplínam. Nielen v minulosti, ale aj v súčastnosti predstavujú
NUMERICKÁ MATEMATIKA. Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ. Fakulta elektrotechniky a informatiky
 Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ NUMERICKÁ MATEMATIKA Fakulta elektrotechniky a informatiky Štefan Berežný Táto publikácia vznikla za finančnej podpory
Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ NUMERICKÁ MATEMATIKA Fakulta elektrotechniky a informatiky Štefan Berežný Táto publikácia vznikla za finančnej podpory
Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich
 Tuesday 15 th January, 2013, 19:53 Základy tenzorového počtu M.Gintner Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich násobenie reálnym číslom tak, že platí:
Tuesday 15 th January, 2013, 19:53 Základy tenzorového počtu M.Gintner Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich násobenie reálnym číslom tak, že platí:
Motivácia pojmu derivácia
 Derivácia funkcie Motivácia pojmu derivácia Zaujíma nás priemerná intenzita zmeny nejakej veličiny (dráhy, rastu populácie, veľkosti elektrického náboja, hmotnosti), vzhľadom na inú veličinu (čas, dĺžka)
Derivácia funkcie Motivácia pojmu derivácia Zaujíma nás priemerná intenzita zmeny nejakej veličiny (dráhy, rastu populácie, veľkosti elektrického náboja, hmotnosti), vzhľadom na inú veličinu (čas, dĺžka)
primitívnoufunkcioukfukncii f(x)=xnamnožinereálnychčísel.avšakaj 2 +1 = x, tedaajfunkcia x2
 Neurčitý integrál. Primitívna funkcia a neurčitý integrál Funkcia F(x)sanazývaprimitívnoufunkcioukfunkcii f(x)naintervale(a,b),akpre každé x (a,b)platí F (x)=f(x). Z definície vidíme, že pojem primitívnej
Neurčitý integrál. Primitívna funkcia a neurčitý integrál Funkcia F(x)sanazývaprimitívnoufunkcioukfunkcii f(x)naintervale(a,b),akpre každé x (a,b)platí F (x)=f(x). Z definície vidíme, že pojem primitívnej
Goniometrické funkcie
 Goniometrické funkcie Oblúková miera Goniometrické funkcie sú funkcie, ktoré sa používajú pri meraní uhlov (Goniometria Meranie Uhla). Pri týchto funkciách sa uvažuje o veľkostiach uhlov udaných v oblúkovej
Goniometrické funkcie Oblúková miera Goniometrické funkcie sú funkcie, ktoré sa používajú pri meraní uhlov (Goniometria Meranie Uhla). Pri týchto funkciách sa uvažuje o veľkostiach uhlov udaných v oblúkovej
Goniometrické substitúcie
 Goniometrické substitúcie Marta Kossaczká S goniometrickými funkciami ste sa už určite stretli, pravdepodobne predovšetkým v geometrii. Ich použitie tam ale zďaleka nekončí. Nazačiatoksizhrňme,čoonichvieme.Funkciesínusakosínussadajúdefinovať
Goniometrické substitúcie Marta Kossaczká S goniometrickými funkciami ste sa už určite stretli, pravdepodobne predovšetkým v geometrii. Ich použitie tam ale zďaleka nekončí. Nazačiatoksizhrňme,čoonichvieme.Funkciesínusakosínussadajúdefinovať
1. POLIA A VEKTOROVÉ PRIESTORY. V tejto kapitole zavedieme dva druhy algebraických štruktúr, ktoré budú hrať v celom
 1. POLIA A VEKTOROVÉ PRIESTORY V tejto kapitole zavedieme dva druhy algebraických štruktúr, ktoré budú hrať v celom ďalšom výklade kľúčovú úlohu, a dokážeme o nich niekoľko jednoduchých základných tvrdení.
1. POLIA A VEKTOROVÉ PRIESTORY V tejto kapitole zavedieme dva druhy algebraických štruktúr, ktoré budú hrať v celom ďalšom výklade kľúčovú úlohu, a dokážeme o nich niekoľko jednoduchých základných tvrdení.
3. Striedavé prúdy. Sínusoida
 . Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
. Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
Obsah. 1.1 Základné pojmy a vzťahy Základné neurčité integrály Cvičenia Výsledky... 11
 Obsah Neurčitý integrál 7. Základné pojmy a vzťahy.................................. 7.. Základné neurčité integrály............................. 9.. Cvičenia..........................................3
Obsah Neurčitý integrál 7. Základné pojmy a vzťahy.................................. 7.. Základné neurčité integrály............................. 9.. Cvičenia..........................................3
p(α 1 ) = u 1. p(α n ) = u n. Definícia (modulárna reprezentácia polynómu). Zobrazenie
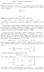 1. Rychlá Fourierová transformácia Budeme značiť teleso T a ω jeho prvok. Veta 1.1 (o interpolácií). Nech α 0, α 1,..., α n sú po dvoch rôzne prvky telesa T[x]. Potom pre každé u 0, u 1,..., u n T existuje
1. Rychlá Fourierová transformácia Budeme značiť teleso T a ω jeho prvok. Veta 1.1 (o interpolácií). Nech α 0, α 1,..., α n sú po dvoch rôzne prvky telesa T[x]. Potom pre každé u 0, u 1,..., u n T existuje
ZÁPISKY Z MATEMATICKEJ ANALÝZY 1
 UNIVERZITA PAVLA JOZEFA ŠAFÁRIKA V KOŠICIACH Prírodovedecká fakulta Ústav matematických vied 4 3 4 n 6 4 3 2 3 2 4 3 6 5 6 7 3 4 2 3 3/5 /2 2/5 /3 /4 /5 /0 d 0/ /0 /5 /4 /3 2/5 6 3 2 3 2 6 5 6 7 3 4 2
UNIVERZITA PAVLA JOZEFA ŠAFÁRIKA V KOŠICIACH Prírodovedecká fakulta Ústav matematických vied 4 3 4 n 6 4 3 2 3 2 4 3 6 5 6 7 3 4 2 3 3/5 /2 2/5 /3 /4 /5 /0 d 0/ /0 /5 /4 /3 2/5 6 3 2 3 2 6 5 6 7 3 4 2
Prechod z 2D do 3D. Martin Florek 3. marca 2009
 Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky MATEMATIKA II. Zbierka riešených a neriešených úloh
 Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky MATEMATIKA II Zbierka riešených a neriešených úloh Anna Grinčová Jana Petrillová Košice 06 Technická univerzita v Košiciach Fakulta
Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky MATEMATIKA II Zbierka riešených a neriešených úloh Anna Grinčová Jana Petrillová Košice 06 Technická univerzita v Košiciach Fakulta
UNIVERZITA MATEJA BELA V BANSKEJ BYSTRICI FAKULTA PRÍRODNÝCH VIED. Pavol Hanzel, Pavel Klenovčan ČÍSLA A POČÍTANIE
 UNIVERZITA MATEJA BELA V BANSKEJ BYSTRICI FAKULTA PRÍRODNÝCH VIED Pavol Hanzel, Pavel Klenovčan ČÍSLA A POČÍTANIE BANSKÁ BYSTRICA 2013 Názov: Čísla a počítanie Autori: Prof. RNDr. Pavol Hanzel, CSc. Doc.
UNIVERZITA MATEJA BELA V BANSKEJ BYSTRICI FAKULTA PRÍRODNÝCH VIED Pavol Hanzel, Pavel Klenovčan ČÍSLA A POČÍTANIE BANSKÁ BYSTRICA 2013 Názov: Čísla a počítanie Autori: Prof. RNDr. Pavol Hanzel, CSc. Doc.
REZISTORY. Rezistory (súčiastky) sú pasívne prvky. Používajú sa vo všetkých elektrických
 REZISTORY Rezistory (súčiastky) sú pasívne prvky. Používajú sa vo všetkých elektrických obvodoch. Základnou vlastnosťou rezistora je jeho odpor. Odpor je fyzikálna vlastnosť, ktorá je daná štruktúrou materiálu
REZISTORY Rezistory (súčiastky) sú pasívne prvky. Používajú sa vo všetkých elektrických obvodoch. Základnou vlastnosťou rezistora je jeho odpor. Odpor je fyzikálna vlastnosť, ktorá je daná štruktúrou materiálu
Tematický výchovno - vzdelávací plán. Cvičenia z matematiky. pre 9. ročník
 výchovno vzdelávací plán Cvičenia z matematiky pre 9. ročník Počet hodín : 1 hod. týždenne Plán bol vypracovaný podľa: ŠVP pre 2. stupeň ZŠ ISCED 2 Plán vypracoval/a: Mgr. Viera Obložinská Školský rok:
výchovno vzdelávací plán Cvičenia z matematiky pre 9. ročník Počet hodín : 1 hod. týždenne Plán bol vypracovaný podľa: ŠVP pre 2. stupeň ZŠ ISCED 2 Plán vypracoval/a: Mgr. Viera Obložinská Školský rok:
1 Úvod Predhovor Sylaby a literatúra Základné označenia... 3
 Obsah 1 Úvod 3 1.1 Predhovor...................................... 3 1.2 Sylaby a literatúra................................. 3 1.3 Základné označenia................................. 3 2 Množiny a zobrazenia
Obsah 1 Úvod 3 1.1 Predhovor...................................... 3 1.2 Sylaby a literatúra................................. 3 1.3 Základné označenia................................. 3 2 Množiny a zobrazenia
Úvod 2 Predhovor... 2 Sylaby a literatúra... 2 Označenia... 2
 Obsah Úvod Predhovor Sylaby a literatúra Označenia Euklidovské vektorové priestory 3 Skalárny súčin 3 Gram-Schmidtov ortogonalizačný proces 8 Kvadratické formy 6 Definícia a základné vlastnosti 6 Kanonický
Obsah Úvod Predhovor Sylaby a literatúra Označenia Euklidovské vektorové priestory 3 Skalárny súčin 3 Gram-Schmidtov ortogonalizačný proces 8 Kvadratické formy 6 Definícia a základné vlastnosti 6 Kanonický
MATEMATIKA 4.OA - 5 h týždenne 165 h ročne školský rok 2014/2015
 MATEMATIKA 4.OA - 5 h týždenne 165 h ročne školský rok 2014/2015 Mgr. Valeria Godovičová 1. Mesiac 1 Úvodná hodina Telo 2-5 Druhá a tretia mocnina - čo už poznáme - opačné čísla a ich mocniny SEPTEMBER
MATEMATIKA 4.OA - 5 h týždenne 165 h ročne školský rok 2014/2015 Mgr. Valeria Godovičová 1. Mesiac 1 Úvodná hodina Telo 2-5 Druhá a tretia mocnina - čo už poznáme - opačné čísla a ich mocniny SEPTEMBER
Spojitosť a limity trochu inak
 Spojitosť a limity trochu inak Štefan Tkačik Abstrakt Spojitosť funkcie alebo oblastí je základným stavebným kameňom matematickej analýzy. Pochopenie jej podstaty uľahčí chápanie diferenciálneho a integrálneho
Spojitosť a limity trochu inak Štefan Tkačik Abstrakt Spojitosť funkcie alebo oblastí je základným stavebným kameňom matematickej analýzy. Pochopenie jej podstaty uľahčí chápanie diferenciálneho a integrálneho
MIDTERM (A) riešenia a bodovanie
 MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
Numerické metódy Učebný text pre bakalárske štúdium
 Imrich Pokorný Numerické metódy Učebný text pre bakalárske štúdium Strana 1 z 48 1 Nepresnosť numerického riešenia úloh 4 1.1 Zdroje chýb a ich klasifikácia................... 4 1.2 Základné pojmy odhadu
Imrich Pokorný Numerické metódy Učebný text pre bakalárske štúdium Strana 1 z 48 1 Nepresnosť numerického riešenia úloh 4 1.1 Zdroje chýb a ich klasifikácia................... 4 1.2 Základné pojmy odhadu
SK skmo.sk. 2009/ ročník MO Riešenia úloh domáceho kola kategórie A
 SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/2010 59. ročník MO Riešenia úloh domáceho kola kategórie A 1. V obore reálnych čísel riešte sústavu rovníc x2 y = z 1, y2 z = x 1, z2 x = y 1. (Radek Horenský) Riešenie.
SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/2010 59. ročník MO Riešenia úloh domáceho kola kategórie A 1. V obore reálnych čísel riešte sústavu rovníc x2 y = z 1, y2 z = x 1, z2 x = y 1. (Radek Horenský) Riešenie.
1-MAT-220 Algebra februára 2012
 1-MAT-220 Algebra 1 12. februára 2012 Obsah 1 Grupy 3 1.1 Binárne operácie.................................. 3 1.2 Cayleyho veta.................................... 3 2 Faktorizácia 5 2.1 Relácie ekvivalencie
1-MAT-220 Algebra 1 12. februára 2012 Obsah 1 Grupy 3 1.1 Binárne operácie.................................. 3 1.2 Cayleyho veta.................................... 3 2 Faktorizácia 5 2.1 Relácie ekvivalencie
MATEMATIKA II ZBIERKA ÚLOH
 TECHNICKÁ UNIVERZITA V KOŠICIACH STAVEBNÁ FAKULTA KATEDRA MATEMATIKY A DESKRIPTÍVNEJ GEOMETRIE RNDr. Pavol PURCZ, PhD. RNDr. Martina RÉVAYOVÁ MATEMATIKA II ZBIERKA ÚLOH KOŠICE 6 Copyright c 6, RNDr. Pavol
TECHNICKÁ UNIVERZITA V KOŠICIACH STAVEBNÁ FAKULTA KATEDRA MATEMATIKY A DESKRIPTÍVNEJ GEOMETRIE RNDr. Pavol PURCZ, PhD. RNDr. Martina RÉVAYOVÁ MATEMATIKA II ZBIERKA ÚLOH KOŠICE 6 Copyright c 6, RNDr. Pavol
7 Derivácia funkcie. 7.1 Motivácia k derivácii
 Híc, P Pokorný, M: Matematika pre informatikov a prírodné vedy 7 Derivácia funkcie 7 Motivácia k derivácii S využitím derivácií sa stretávame veľmi často v matematike, geometrii, fyzike, či v rôznych technických
Híc, P Pokorný, M: Matematika pre informatikov a prírodné vedy 7 Derivácia funkcie 7 Motivácia k derivácii S využitím derivácií sa stretávame veľmi často v matematike, geometrii, fyzike, či v rôznych technických
DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c)
 Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach Božena Mihalíková, Ivan Mojsej Strana 1 z 43 DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c) 1 Obyčajné diferenciálne rovnice 3 1.1 Úlohy
Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach Božena Mihalíková, Ivan Mojsej Strana 1 z 43 DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c) 1 Obyčajné diferenciálne rovnice 3 1.1 Úlohy
Riešenia. Základy matematiky. 1. a) A = { 4; 3; 2; 1; 0; 1; 2; 3}, b) B = {4; 9; 16}, c) C = {2; 3; 5},
 Riešenia Základy matematiky 1. a) A = { ; ; ; 1; 0; 1; ; }, b) B = {; 9; 16}, c) C = {; ; 5}, d) D = { 1}, e) E =.. B, C, D, F (A neobsahuje prvok 1, E obsahuje navyše prvok 1, G neobsahuje prvok 1)..
Riešenia Základy matematiky 1. a) A = { ; ; ; 1; 0; 1; ; }, b) B = {; 9; 16}, c) C = {; ; 5}, d) D = { 1}, e) E =.. B, C, D, F (A neobsahuje prvok 1, E obsahuje navyše prvok 1, G neobsahuje prvok 1)..
Učebný zdroj pre žiakov z predmetu Matematika
 STREDNÁ ODBORNÁ ŠKOLA Komenského 6, 08 7 Lipany Učebný zdroj pre žiakov z predmetu Matematika Odbor: Kozmetik a Pracovník marketingu Autorka: PaedDr. Iveta Štefančínová, Ph.D. Moderné vzdelávanie pre vedomostnú
STREDNÁ ODBORNÁ ŠKOLA Komenského 6, 08 7 Lipany Učebný zdroj pre žiakov z predmetu Matematika Odbor: Kozmetik a Pracovník marketingu Autorka: PaedDr. Iveta Štefančínová, Ph.D. Moderné vzdelávanie pre vedomostnú
Testy a úlohy z matematiky
 Testy a úlohy z matematiky Spracovala a zostavila: c Mgr. Hedviga Soósová 008 Vydavateľ: Copyright c VARIA PRINT, s. r. o. 008. Prvé vydanie. Kontakt: VARIA PRINT, s. r. o. Mgr. Marta Varsányiová Ul. františkánov
Testy a úlohy z matematiky Spracovala a zostavila: c Mgr. Hedviga Soósová 008 Vydavateľ: Copyright c VARIA PRINT, s. r. o. 008. Prvé vydanie. Kontakt: VARIA PRINT, s. r. o. Mgr. Marta Varsányiová Ul. františkánov
Matematika 1 Elementárny kalkulus
 Matematika Elementárny kalkulus Úvod Prehl ad. Tieto poznámky obsahujú podklady k prednáške Matematika na špecializácii Aplikovaná informatika: jedná sa o 2 dvojhodinových prednášok doplnených dvojhodinovými
Matematika Elementárny kalkulus Úvod Prehl ad. Tieto poznámky obsahujú podklady k prednáške Matematika na špecializácii Aplikovaná informatika: jedná sa o 2 dvojhodinových prednášok doplnených dvojhodinovými
9 Neurčitý integrál. 9.1 Primitívna funkcia a neurčitý integrál. sa nazýva primitívnou funkciou k funkcii f ( x) každé x ( a,
 Hí, P Pokorný, M: Maemaika pre informaikov a prírodné vedy 9 Neurčiý inegrál 9 Primiívna funkia a neurčiý inegrál Funkia F sa nazýva primiívnou funkiou k funkii f na inervale ( b) každé ( a, b) plaí F
Hí, P Pokorný, M: Maemaika pre informaikov a prírodné vedy 9 Neurčiý inegrál 9 Primiívna funkia a neurčiý inegrál Funkia F sa nazýva primiívnou funkiou k funkii f na inervale ( b) každé ( a, b) plaí F
Základná škola Jána Hollého s materskou školou Madunice. Prehľad učiva matematiky. základnej školy
 Základná škola Jána Hollého s materskou školou Madunice Prehľad učiva matematiky základnej školy Obsah strana 1. Prirodzené, celé, racionálne, reálne čísla... 1 2. Operácie s racionálnymi číslami... 2
Základná škola Jána Hollého s materskou školou Madunice Prehľad učiva matematiky základnej školy Obsah strana 1. Prirodzené, celé, racionálne, reálne čísla... 1 2. Operácie s racionálnymi číslami... 2
