qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj
|
|
|
- Ματθίας Ακρίδας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ klzxcvλοπbnαmqwertyuiopasdfghjklz ΤΕΛΙΚΗ ΕΠΑΝΑΛΗΨΗ xcvbnmσγqwφertyuioσδφpγρaηsόρ ωυdfghjργklαzxcvbnβφδγωmζqwert λκοθξyuiύασφdfghjklzxcvbnmqwerty uiopaβsdfghjklzxcεrυtγyεuνiιoαpasdf ghjklzxcηvbnασφδmqwertασδyuiopa sdfασδφγθμκxcvυξσφbnmσφγqwθeξ τσδφrtyuφγςοιopaασδφsdfghjklzxcv ασδφbnγμ,mqwertyuiopasdfgασργκο ϊτbnmqwertyσδφγuiopasσδφγdfghjk lzxσδδγσφγcvbnmqwertyuioβκσλπp asdfghjklzxcvbnmqwertyuiopasdγαε ορlzxcvbnmqwertyuiopasdfghjkαεργ αεργαγρqwertyuiopasdfghjklzxασδφ mοιηξηωχψφσuioψασεφγvbnmqwer tyuiopasdfghjklzxcvbnmqwertyuiopσ
2 ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 1) Τι λέγεται γραμμική εξίσωση και τι παριστάνει; Γραμμική εξίσωση λέγεται η εξίσωση, με ή, η οποία παριστάνει μια ευθεία γραμμή. ) Τι μορφή έχει η εξίσωση όταν,, και τι παριστάνει ; Αν,,, τότε η εξίσωση γράφεται : Στην περίπτωση αυτή η εξίσωση παριστάνει ευθεία που έχει συντελεστή διεύθυνσης. Η ευθεία τέμνει τον άξονα άξονα στο. στο και τον 3) Τι μορφή έχει η εξίσωση όταν, και και τι παριστάνει ; Αν, και τότε η εξίσωση γράφεται : Στην περίπτωση αυτή η εξίσωση παριστάνει ευθεία που διέρχεται από την αρχή των αξόνων και έχει συντελεστή διεύθυνσης. []
3 4) Τι μορφή έχει η εξίσωση όταν, με και ; Αν και, τότε η εξίσωση γράφεται : Στην περίπτωση αυτή η εξίσωση παριστάνει ευθεία που είναι παράλληλη στον άξονα και τέμνει τον άξονα στο σημείο. 5) Τι μορφή έχει η εξίσωση όταν, με και ; Αν και, τότε η εξίσωση γράφεται : Στην περίπτωση αυτή η εξίσωση παριστάνει ευθεία που είναι παράλληλη στον άξονα και τέμνει τον άξονα στο σημείο. ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 1) Τι λέγεται γραμμικό σύστημα x; Όταν έχουμε δύο γραμμικές εξισώσεις και και ζητάμε τις κοινές λύσεις αυτών, τότε λέμε ότι έχουμε να λύσουμε ένα γραμμικό σύστημα δύο εξισώσεων με δύο αγνώστους ή, πιο σύντομα, ένα γραμμικό σύστημα x και γράφουμε αx γ ) Τι λέγεται λύση ενός γραμμικού συστήματος x; Κάθε ζεύγος αριθμών που επαληθεύει και τις δύο εξισώσεις του συστήματος λέγεται λύση του συστήματος. [3]
4 ΛΥΣΗ ΚΑΙ ΔΙΕΡΕΥΝΗΣΗ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ x 1) Τι λέγεται ορίζουσα του συστήματος και τι ορίζουσα των αγνώστων ; αx γ = Η ορίζουσα του συστήματος. = Η ορίζουσα που προκύπτει αν στη θέση των συντελεστών του x άλουμε τους σταθερούς όρους. = Η ορίζουσα που προκύπτει αν στη θέση των συντελεστών του y άλουμε τους σταθερούς όρους. Μεθοδολογία επίλυσης ενός x γραμμικού συστήματος με τη μέθοδο των οριζουσών. Υπολογίζουμε τις ορίζουσες,,. Βρίσκουμε τις τιμές της παραμέτρου, για τις οποίες είναι D = 0. Διακρίνουμε τις περιπτώσεις: Αν D, τότε το σύστημα έχει μοναδική λύση (x, ), με: και Αν D, τότε το σύστημα ή είναι αδύνατο ή έχει άπειρες λύσεις. Aν D και ή τότε το σύστημα είναι αδύνατο. Aν D τότε το σύστημα έχει άπειρες λύσεις, Εκτός αν και ή, οπότε το σύστημα είναι αδύνατο. [4]
5 Παρατήρηση: Κάθε σύστημα της μορφής : αx ονομάζεται ομογενές και δεν είναι ποτέ αδύνατο. Έχει λύση πάντα τη μηδενική (, ) (, )και εξετάζουμε αν έχει και άλλες λύσεις εκτός από τη μηδενική. I. Αν D το σύστημα έχει μοναδική λύση την μηδενική. II. Αν D το σύστημα έχει άπειρες λύσεις στις οποίες ανήκει και η μηδενική. ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΜΕ ΠΕΡΙΣΣΟΤΕΡΟΥΣ ΑΠΟ ΔΥΟ ΑΓΝΩΣΤΟΥΣ 1) Τι λέγεται γραμμική εξίσωση γραμμική εξίσωση με τρεις αγνώστους ; Μία εξίσωση της μορφής αx γz, με έναν τουλάχιστον από τους συντελεστές α,, γ διάφορο του μηδενός, λέγεται γραμμική εξίσωση με τρεις αγνώστους. )Τι λέγεται λύση μιας γραμμικής εξίσωσης με τρεις αγνώστους ; Λύση μιας γραμμικής εξίσωσης με τρεις αγνώστους λέγεται κάθε τριάδα αριθμών που την επαληθεύει. 3) Τι λέγεται γραμμικό σύστημα 3x3; Όταν έχουμε τρεις γραμμικές εξισώσεις με τρεις αγνώστους: α1x 1y γ1z δ1, α x y γ z δ και α3 x 3 y γ3 z δ3 και ζητάμε τις κοινές λύσεις τους, τότε λέμε ότι έχουμε να λύσουμε ένα γραμμικό σύστημα τριών εξισώσεων με τρεις αγνώστους ή, πιο σύντομα, ένα γραμμικό σύστημα 3 x 3 και γράφουμε ΜΗ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 1) Τι λέγεται μη γραμμικό σύστημα; Μη γραμμικό σύστημα λέγεται εκείνο το σύστημα όπου μία τουλάχιστον εξίσωση δεν είναι γραμμική. Τα μη γραμμικά συστήματα συνήθως τα λύνουμε με τη μέθοδο της αντικατάστασης ή με τη οήθεια της αλλαγής μετα λητής. [5]
6 ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ ΜΟΝΟΤΟΝΙΑ-ΑΚΡΟΤΑΤΑ ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ 1) Πότε μια συνάρτηση f λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της; Μια συνάρτηση fλέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε, Є Δ με ισχύει : ( ) ( ). ) Πότε μια συνάρτηση f λέγεται γνησίως φθίνουσα σε ένα διάνυσμα Δ του πεδίου ορισμού της; Μια συνάρτηση f λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε, Є Δ με ισχύει : ( ) ( ). Η συνάρτηση ( ) με α είναι γνησίως αύξουσα στο R. Η συνάρτηση ( ) με α είναι γνησίως φθίνουσα στο R. 3) Πότε μία συνάρτηση λέγεται γνησίως μονότονη; Μια συνάρτηση που είναι είτε γνησίως αύξουσα είτε γνησίως φθίνουσα σε ένα διάστημα Δ λέγεται γνησίως μονότονη στο Δ. ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ 1) Πότε λέμε ότι μια συνάρτηση f, με πεδίο ορισμού Α, παρουσιάζει στο x A ελάχιστο; ΡΙ Μια συνάρτηση f, με πεδίο ορισμού ένα σύνολο Α, λέμε ότι παρουσιάζει στο x0 A (ολικό) ελάχιστο όταν: ( ) ( ), για κάθε. Το A λέγεται θέση ελαχίστου, ενώ το ( ) ολικό ελάχιστο ή απλώς ελάχιστο της συνάρτησης f. (ολικό) [6]
7 ) Πότε λέμε ότι μια συνάρτηση f, με πεδίο ορισμού Α, παρουσιάζει στο x A μέγιστο; ΟΡ (ολικό) Μια συνάρτηση f, με πεδίο ορισμού ένα σύνολο Α, λέμε ότι παρουσιάζει στο x0 A (ολικό) μέγιστο όταν: ( ) ( ), για κάθε x A. Το x0 A λέγεται θέση μεγίστου, ενώ το ( )ολικό μέγιστο ή απλώς μέγιστο της. Το (ολικό) μέγιστο και το (ολικό) ελάχιστο μιας συνάρτησης λέγονται ολικά ακρότατα αυτής. ΑΡΤΙΑ ΠΕΡΙΤΤΗ ΣΥΝΑΡΤΗΣΗ 1) Πότε μια συνάρτηση, με πεδίο ορισμού ένα σύνολο Α, λέγεται άρτια; Μια συνάρτηση, με πεδίο ορισμού ένα σύνολο Α, θα λέγεται άρτια, όταν για κάθε ισχύει: και ( ) ( ). Η γραφική παράσταση μιας άρτιας συνάρτησης έχει άξονα συμμετρίας τον άξονα. ) Πότε μια συνάρτηση f, με πεδίο ορισμού ένα σύνολο Α λέγεται περιττή; Μια συνάρτηση f, με πεδίο ορισμού ένα σύνολο Α, θα λέγεται περιττή, όταν για κάθε ισχύει: και ( ) ( ). Η γραφική παράσταση μιας περιττής συνάρτησης έχει κέντρο συμμετρίας την αρχή των αξόνων. ΠΑΡΑΤΗΡΗΣΗ: Το πεδίο ορισμού μιας άρτιας ή περιττής συνάρτησης πρέπει να είναι «συμμετρικό» ως προς το μηδέν, γιατί αν περιέχει το x πρέπει να περιέχει και το x. π.χ. R, R*, R-{5,-5}, [-10,10], (-, ) Σε αντίθετη περίπτωση η συνάρτηση δεν είναι ούτε άρτια ούτε περιττή. Για ν.δ.ο. μια συνάρτηση είναι άρτια ή περιττή: 1) Βρίσκουμε το πεδίο ορισμού της και εξετάζουμε αν είναι «συμμετρικό» ως προς το μηδέν, εξασφαλίζοντας ότι Є, Є. ) Αποδεικνύουμε ότι ( ) ( ), Є. ή ( ) ( ), Є αντίστοιχα. Η συνάρτηση δεν είναι ούτε άρτια ούτε περιττή αν ένα από τα παραπάνω ήματα δεν καταλήξει θετικά. [7]
8 ΚΑΤΑΚΟΡΥΦΗ -ΟΡΙΖΟΝΤΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΜΠΥΛΗΣ Έστω συνάρτηση f με γραφική παράσταση. H γραφική παράσταση της συνάρτησης : ( ) ( ), θα είναι μετατοπισμένη κατά c μονάδες κατακόρυφα προς τα πάνω. ( ) ( ), θα είναι μετατοπισμένη κατά c μονάδες κατακόρυφα προς τα κάτω. ( ) ( ), θα είναι μετατοπισμένη κατά c μονάδες οριζόντια προς τα δεξιά. ( ) ( ), θα είναι μετατοπισμένη κατά c μονάδες οριζόντια προς τα αριστερά. ΤΡΙΓΩΝΟΜΕΤΡΙΑ Τριγωνομετρικοί αριθμοί οξείας γωνίας (0 ο ω 9 ο ) σε ορθογώνιο τρίγωνο έ ά ά = ί AB = BΓ = ί ά ά ί AΓ = ΒΓ έ ά ά = ί ά ά ί ά ά = έ ά ά AB = ΑΓ AΓ = ΑΒ [8]
9 ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ ω, 0 ο ω 36 ο Έστω ορθοκανονικό σύστημα αξόνων. Αν ημιάξονας Οx στραφεί κατά τη θετική φορά (αντίθετα με τους δείκτες του ρολογιού) μέχρι τη θέση Οz, τότε διαγράφει τη γωνία ω. Στο ορθογώνιο τρίγωνο ΟΑ Μ που σχηματίζεται είναι : και (ΟΜ ) x y 0 y =, ρ x =, ρ y =, x x =. y Έτσι αν ο ημιάξονας Οx ο οποίος ονομάζεται αρχική πλευρά κινηθεί μέχρι τη θέση Οz (τελική πλευρά), τότε παράγει μια γωνία ω. Αν Μ(x, y) σημείο της Oz και (ΟΜ) ρ x y 0, τότε ορίζουμε: y x,, ρ ρ x x y y x 0, y 0 ΑΚΤΙΝΙΟ Έστω κύκλος(ο, R). Ακτίνιο ( ) λέγεται το τόξο που έχει μήκος ίσο με την ακτίνα R του κύκλου. Τα τόξα τα μετράμε σε μοίρες ή σε ακτίνια. Η σχέση που συνδέει ένα τόξο μ 0 και α rad είναι α μ 0 π 180 π.. Από τη σχέση αυτή ολόκληρος ο κύκλος είναι τόξο 36 ο και αντιστοιχεί σε τόξο [9]
10 ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ ω ΜΕΓΑΛΥΤΕΡΗΣ ΑΠΟ 36 Αν η γωνία δίνεται σε μοίρες: Για κάθε κ Ζ ισχύει: (. ) (. ) (. ) (. ) Αν η γωνία δίνεται σε : Για κάθε κ Ζ ισχύει: ( ) ( ) ( ) ( ) ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΣ ΚΥΚΛΟΣ Τριγωνομετρικός κύκλος λέγεται ο κύκλος που έχει κέντρο το σημείο Ο(, ) ενός ορθοκανονικού συστήματος αξόνων(αρχή αξόνων) και ακτίνα ρ 1. Οπότε για κάθε γωνία ω ισχύει ότι: 1 1, 1 1 Ο μνημονικός κανόνας( αριθμών. )αναφέρεται στα θετικά πρόσημα των τριγωνομετρικών [10]
11 ΒΑΣΙΚΟΙ ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ Γωνία 30 ο 45 ο 60 ο 90 ο 180 ο 70 ο 360 ο Τριγ. ω αριθμός π 3 π ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ 1. ημ ω συν ω 1 (ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΤΗΣ ΤΡΙΓΩΝΟΜΕΤΡΙΑΣ). ημω συνω, συνω και,. συνω ημω Άρα 1 και 1 4. Σχέσεις που δίνουν το και το συνω συναρτήσει της είναι: ημ ω εφ ω 1 εφ ω συν ω 1 1 εφ ω [11]
12 ΑΠΟΔΕΙΞΕΙΣ 1. ημ ω συν ω 1 Αν (, ) είναι το σημείο όπου η τελική πλευρά της γωνίας ω τέμνει τον τριγωνομετρικό κύκλο, τότε θα είναι :. Επειδή όμως, ( ) 1 και ( ) Θα ισχύει : 1 Οπότε θα έχουμε : 1. Στο ίδιο σχήμα έχουμε : (εφόσον ) (εφόσον ) Γνωρίζουμε ότι : Επομένως : (εφόσον ) (εφόσον ). 1 [1]
13 ΑΝΑΓΩΓΗ ΣΤΟ 1ο ΤΕΤΑΡΤΗΜΟΡΙΟ ΕΙΔΗ ΓΩΝΙΩΝ Αντίθετες Παραπληρωματικές Γωνίες διαφοράς π Γωνίες με άθροισμα π -ω π-ω π ω π-ω Συμπληρωματικές Γωνίες διαφοράς Γωνίες με άθροισμα Γωνίες διαφοράς π π 3π 3π ω ω ω ω ΓΩΝΙΕΣ ΤΡΙΓΩΝΟΥ Επειδή για τις γωνίες έχουμε Α Β Γ 18, τότε Α Β 18 - Γ, οπότε: ( ) (18 ) ( ) (18 ) ( ) (18 ) ( ) (18 ) [13]
14 Επίσης, έχουμε: Α Β Γ Α Β 90 ο 90 ο Γ οπότε: Α 0 Β ημ 90 Γ συν Γ συν ΑΒ 0 Γ Γ 90 εφ Α 0 Β εφ 90 Γ σφ Γ ΑΒ 0 Γ Γ φ 90 εφ Ο τριγωνομετρικός αριθμός παραμένει ίδιος αν η γωνία x είναι της μορφής π ω ή π ω, ενώ : «αλλάζει» όταν η γωνία x είναι της μορφής εφαπτομένη συνεφαπτομένη. ω ή 3 ω : ημίτονο συνημίτονο Το πρόσημο του αποτελέσματος εξαρτάται από το πρόσημο του τριγωνομετρικού αριθμού που μας έδωσαν στο τεταρτημόριο στο οποίο ρίσκεται η τελική πλευρά της γωνίας. Όταν τα τόξα έχουν αρνητικό για οποιαδήποτε γωνία του π, τότε πρώτα γάζουμε το (-) με άση το πρόσημο των αντίθετων γωνιών και στη συνέχεια εργαζόμαστε σύμφωνα με τις προηγούμενες μεθοδολογίες. Περιττά πολλαπλάσια του π,, Άρτια πολλαπλάσια του π, 3,, 3 [14]
15 ΟΙ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Περιοδική συνάρτηση 1) Πότε μια συνάρτηση με πεδίο ορισμού Α λέγεται περιοδική ; Μια συνάρτηση f με πεδίο ορισμού Α λέγεται περιοδική, όταν υπάρχει πραγματικός αριθμός Τ τέτοιος ώστε για κάθε x Α να ισχύει:, ( ) ( ) ( ) Ο αριθμός Τ λέγεται περίοδος της συνάρτησης f. Πεδίο ορισμού: R Σύνολο τιμών: ( ) 1, 1 Περιοδική με περίοδο: Μελέτη τριγωνομετρικών συναρτήσεων Α) Η συνάρτηση ( ) Η ( ) είναι περιττή αφού R και ( ) ( ) ( ) Άρα η γραφική της παράσταση είναι συμμετρική ως προς το (, ). 3 Η ( ) παρουσιάζει μέγιστο 1 για x = και ελάχιστο 1 για x = H ( ) είναι : γνησίως αύξουσα για x 0,, γνησίως φθίνουσα για x, 3 3 γνησίως φθίνουσα για x,, γνησίως αύξουσα για x, Γραφική παράσταση: [15]
16 Β) Η συνάρτηση f(x) συνx Πεδίο ορισμού: R. Σύνολο τιμών: ( ) 1, 1. Περιοδική με περίοδο:. Η ( ) είναι άρτια αφού Α R και ( ) ( ) ( ). Άρα η γραφική της παράσταση είναι συμμετρική ως προς τον. Η ( ) παρουσιάζει : μέγιστο 1 για και και ελάχιστο 1 για x π. Η f(x) συνx είναι γνησίως φθίνουσα για x 0,, γνησίως φθίνουσα για x,, 3 3 γνησίως αύξουσα για x,, και γνησίως αύξουσα για x, Γραφική παράσταση: [16]
17 Γ) Η συνάρτηση f(x) εφx Πεδίο ορισμού Σύνολο τιμών ( ) R. Περιοδική με περίοδο., Άρα τη f(x) εφx τη μελετούμε σε διάστημα πλάτους π, π.χ. στο,. Η f(x) εφx είναι περιττή. Ακρότατα δεν υπάρχουν. Η f(x) εφx είναι γνησίως αύξουσα για x, Οι κατακόρυφες ευθείες γραφικής παράστασης και είναι κατακόρυφες ασύμπτωτες της Γραφική παράσταση: [17]
18 ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ή, -1 α 1 ή, 1 1,, ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΑΘΡΟΙΣΜΑΤΟΣ ΚΑΙ ΔΙΑΦΟΡΑΣ ΓΩΝΙΩΝ ( ), ( ) ( ), ( ) ( ) 1 ( ) ( ) ( ) π,,,.,,. [18]
19 ΤΥΠΟΙ ΓΩΝΙΑΣ α ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΤΗΣ ΓΩΝΙΑΣ α 1 1 ό 1 π π, ΤΥΠΟΙ ΑΠΟΤΕΤΡΑΓΩΝΙΣΜΟΥ ημ α συν α εφ α ΤΥΠΟΙ ΤΟΥ α Αν στους τύπους που έχουμε δώσει από την αρχή αντικαταστήσουμε όπου α α και όπου α α, προκύπτουν οι παρακάτω τύποι: α α α α α 1 1 α, 1 α 1 α 1 εφ α α 1 1 Αρκετά χρήσιμοι σε ορισμένες ασκήσεις είναι οι παρακάτω τύποι: ημ3α 3ημα 4ημ 3 α, συν3α 4συν 3 α - 3συνα και οι τύποι που μας δίνουν το ημα και συνα συναρτήσει της : ημα 1 συνα 1 1 [19]
20 ΠΟΛΥΩΝΥΜΑ Ορισμοί Μονώνυμο του : ονομάζεται κάθε παράσταση της μορφής αx v, όπου α R, v N και x μια μετα λητή που μπορεί να πάρει οποιαδήποτε τιμή από το R. Πολυώνυμο του : ονομάζεται κάθε παράσταση της μορφής Ρ(x) ανx v αν-1x v-1... α1x α0, όπου α0, α1,..., αν είναι πραγματικοί αριθμοί και ν φυσικός αριθμός. Βαθμός ενός πολυωνύμου Ρ(x) ονομάζεται ο εκθέτης της μεγαλύτερης δύναμης του με συντελεστή διάφορο του μηδενός. Ρίζα ενός πολυωνύμου Ρ(x) λέγεται ο αριθμός που μηδενίζει το πολυώνυμο. Δηλαδή αν ο αριθμός ρ είναι ρίζα του πολυωνύμου Ρ(x), τότε Ρ(ρ). Αριθμητική τιμή ενός πολυωνύμου Ρ(x) λέγεται ο αριθμός που προκύπτει αν στο Ρ(x) αντικαταστήσουμε το χ με μια τιμή χ0. Δύο πολυώνυμα Ρ(x), Q(x) θα λέγονται ίσα αν και μόνο αν είναι του ίδιου αθμού και οι. συντελεστές των ομο αθμίων όρων τους είναι ίσοι. ΘΕΩΡΗΜΑ (ταυτότητα της διαίρεσης) Για κάθε ζεύγος πολυωνύμων Δ(x) και δ(x) και υ(x) για τα οποία ισχύει: Δ(x) δ(x). π(x) υπάρχει μοναδικό ζεύγος πολυωνύμων π(x) υ(x) Δ(x) υ(x) δ(x) π(x) [0]
21 ΘΕΩΡΗΜΑ Ένα πολυώνυμο ( ) έχει παράγοντα το x - ρ αν και μόνο αν το ρ είναι ρίζα του Ρ(x), δηλαδή αν και μόνο αν ( )= 0 ΠΑΡΑΤΗΡΗΣΕΙΣ 1) Το υπόλοιπο της διαίρεσης του ( ): ( ) ισούται με την αριθμητική τιμή του πολυωνύμου για x ρ δηλαδή ( ). ) Αν το x - ρ είναι παράγοντας του ( ), τότε: ( ),και ( ). 3) Αν η διαίρεση του ( ) με το x - ρ είναι τέλεια, τότε: ( ) ( ) ( ) Το (x-ρ) είναι παράγοντας του ( ) ( ). 4) Αν το υπόλοιπο της διαίρεσης του ( ) με το x - ρ είναι μηδέν, δηλαδή υ Ρ(ρ), τότε Το ( ) είναι παράγοντας του ( ) ( ) ( ) ( ) Σημείωση: Γενικά, αν σε μια διαίρεση είναι υ(x), τότε η διαίρεση λέγεται τέλεια και η ταυτότητα της διαίρεσης γράφεται ( ) ( ) ( ) Στην περίπτωση αυτή λέμε ότι το δ(x) διαιρεί το Δ(x) ή ότι το δ(x) είναι παράγοντας του ( ) ή ότι το ( ) διαιρείται με το ( ) ή ακόμη ότι το ( ) είναι διαιρέτης του ( ). [1]
22 Σχήμα Horner Το σχήμα Horner είναι μια μέθοδος, με τη οήθεια της οποίας μπορούμε: 1. Να κάνουμε την διαίρεση ενός πολυωνύμου Ρ(x) με το (x - ρ) και να ρούμε το πηλίκο και το υπόλοιπο της διαίρεσης.. Να διαπιστώσουμε αν ένας αριθμός ρ είναι ρίζα του πολυωνύμου Ρ(x) ή ισοδύναμα να διαπιστώσουμε αν το (x - ρ)είναι παράγοντας του Ρ(x). 3. Να ρούμε την αριθμητική τιμή του Ρ (x) για x ρ 4. Να παραγοντοποιήσουμε ένα πολυώνυμο. Θεώρημα ακεραίων ριζών Έστω η πολυωνυμική εξίσωση ανx ν αv-1x v-1... α1x α0 με ακέραιους συντελεστές. Αν ο ακέραιος ρ είναι ρίζα της εξίσωσης, τότε ο ρ είναι διαιρέτης του σταθερού όρου α0. Κεφάλαιο 4 ο Αποδείξεις Θεωρημάτων ΘΕΩΡΗΜΑ: Το υπόλοιπο της διαίρεσης ενός πολυωνύμου ( ) με το τιμή του πολυωνύμου για. Είναι δηλαδή ( ). είναι ίσο με την ΑΠΟΔΕΙΞΗ Η ταυτότητα της διαίρεσης του πολυωνύμου ( ) με το πολυώνυμο x-p γράφεται. ( ) ( ) ( ) ( ) Επειδή ο διαιρέτης x-p είναι πρώτου αθμού, το υπόλοιπο της διαίρεσης θα είναι ένα σταθερό πολυώνυμο. Έτσι έχουμε: ( ) ( ) ( ) και, αν θέσουμε x=p, παίρνουμε ( ) ( ) ( ) Επομένως ( ) ( ) ( ) ( ) []
23 ΘΕΩΡΗΜΑ: Ένα πολυώνυμο ( ) έχει παράγοντα x-ρ αν και μόνο αν το ρ είναι ρίζα του Ρ(x), δηλαδή αν και μόνο αν ( ). ΑΠΟΔΕΙΞΗ Έστω ότι το x-ρ είναι παράγοντας του ( ). Τότε ( ) ( ) ( ) από την ισότητα αυτή για παίρνουμε ( ) ( ) ( ), που σημαίνει ότι το ρ είναι ρίζα του Ρ(x). Αντιστρόφως: Έστω ότι το ρ είναι ρίζα του Ρ(x), δηλαδή ισχύει Ρ(ρ), οπότε από τη σχέση ( ) ( ) ( ) ( ) παίρνουμε ( ) ( ) ( ), που σημαίνει ότι το x-ρ είναι παράγοντας του ( ). ΘΕΩΡΗΜΑ (ακέραιων ριζών) Έστω η πολυωνυμική εξίσωση ανx v αν-1x ν-1... α1x α0, με ακέραιους συντελεστές. Αν ο ακέραιος ρ είναι ρίζα της εξίσωσης, τότε ο ρ είναι διαιρέτης του σταθερού όρου α0. ΑΠΟΔΕΙΞΗ Αν ο ρ είναι ρίζα της εξίσωσης, τότε διαδοχικά έχουμε ανρ ν αν-1ρ ν-1... α1ρ α0=0 α0=-ανρ ν -αν-1ρ ν α1ρ α0 ρ(-ανρ ν-1 -αν-1ρ ν α1) Επειδή οι ρ, α1,α,...,αν είναι ακέραιοι έπεται ότι και ο ανρ ν-1 -αν-1ρ ν α1 είναι ακέραιος. Από την τελευταία ισότητα συμπεραίνουμε, ότι ο ρ είναι διαιρέτης του α0. [3]
24 ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ Αν α και α 1. αντιστοιχίζοντας κάθε x R στη δύναμη α x ορίζουμε τη συνάρτηση : R Rμε τύπο ( ), η οποία λέγεται εκθετική συνάρτηση με άση α. Αν 1, τότε έχουμε ( ) 1 x 1, δηλαδή προκύπτει η σταθερή συνάρτηση ( ) 1. Aνάλογα με τη άση α διακρίνουμε δύο περιπτώσεις: Αν α 1 τότε για τη συνάρτηση έχουμε: Πεδίο ορισμού το R. Σύνολο τιμών το (, ). Γνησίως αύξουσα στο R, δηλαδή αν Είναι «1-1», δηλαδή Τέμνει τον y y στο (,1), ενώ δεν τέμνει τον x x. Πλησιάζει τον αρνητικό ημιάξονα Οx χωρίς να τον τέμνει. (ασύμπτωτη της γραφικής παράστασης) Αν α 1 τότε για τη συνάρτηση έχουμε: Πεδίο ορισμού το R. Σύνολο τιμών το (0,+ ). Γνησίως φθίνουσα στο R, δηλαδή αν Είναι «1-1», δηλαδή Τέμνει τον y y στο (,1), ενώ δεν τέμνει τον x x. Πλησιάζει τον θετικό ημιάξονα Οx χωρίς να τον τέμνει (ασύμπτωτη της γραφικής παράστασης). Ο αριθμός e. Η εκθετική συνάρτηση με άση το e είναι f(x) = e x και έχει τις ίδιες ιδιότητες με την εκθετική συνάρτηση που έχει άση μεγαλύτερη του 1. [4]
25 ΛΟΓΑΡIΘΜΟΙ Ο logα θ είναι ο αριθμός στον οποίο πρέπει να υψώσουμε τον α για να ρούμε το θ. Ισχύει η ισοδυναμία: α x θ x = logα θ. Από τον ορισμό του λογαρίθμου προκύπτει ότι: 1 1 Ιδιότητες λογαρίθμων Αν θ1, θ, θ, α 1 και κ R, αποδεικνύεται ότι: 1. ( 1. θ) = θ1 + θ. = θ1 - θ 3. θ κ κ. θ Δεκαδικοί λογάριθμοι Αν η άση του λογαρίθμου είναι α 1. τότε ο log10 θ συμ ολίζεται log θ και λέγεται δεκαδικός ή κοινός λογάριθμος. Ισχύει η ισοδυναμία: logθ x 10 x θ Φυσικοί λογάριθμοι Αν η άση του λογαρίθμου είναι α e, τότε ο λογάριθμος ενός θετικού αριθμού θ συμ ολίζεται nθ και λέγεται φυσικός ή νεπέριος λογάριθμος. Ισχύει η ισοδυναμίαnθ x e x θ Τύπος αλλαγής άσης Αν α, με α, 1 και θ, τότε αποδεικνύεται ότι: = log log α α [5]
26 ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ Γνωρίζουμε την εκθετική συνάρτηση ( ) α x η οποία είναι «1-1». Από την ισοδυναμία α x = y x = logαy ορίζεται η αντίστροφη συνάρτηση f -1 (y) = logαy, η οποία ονομάζεται λογαριθμική συνάρτηση. Οι γραφικές παραστάσεις της εκθετικής και λογαριθμικής συνάρτησης είναι συμμετρικές ως προς την y = x, επειδή η μία είναι αντίστροφη της άλλης. Για τη συνάρτηση φ (x) logαx με α 1, έχουμε: Πεδίο ορισμού το (, ). Σύνολο τιμών το R. Είναι γνησίως αύξουσα δηλαδή για κάθε x1,x (0,+ ) με Είναι «1-1», δηλαδή αν Τέμνει τον στο (1, ), ενώ δεν τέμνει τον Πλησιάζει τον αρνητικό ημιάξονα Οy χωρίς να τοντέμνει (ασύμπτωτη της γραφικής παράστασης). [6]
27 Κεφάλαιο 5ο ΙΔΙΟΤΗΤΕΣ ΛΟΓΑΡΙΘΜΩΝ ΑΠΟΔΕΙΞΕΙΣ Αν θ1, θ, θ, α 1 και κ R, αποδεικνύεται ότι: 1. ( 1. θ) = θ1 + θ. = θ1 - θ 3. θ κ κ. θ 1. Έστω ότι είναι: 1 και (1) Τότε έχουμε: 1 και οπότε: 1 δηλαδή 1 Από το ορισμό όμως του λογάριθμου, η τελευταία ισότητα είναι ισοδύναμη με την ( 1. θ)= από την οποία, λόγω των (1), έχουμε τελικά: ( 1. θ) = θ1 + θ. Έστω ότι είναι: 1 και (1) Tότε έχουμε : 1 και οπότε: : δηλαδή Από το ορισμό όμως του λογάριθμου, η τελευταία ισότητα είναι ισοδύναμη με την = από την οποία, λόγω των (1), έχουμε τελικά: = θ1 - θ 3. Έστω ότι είναι: : θ Tότε έχουμε : οπότε: Aπό τον ορισμό όμως του λογάριθμου, η τελευταία ισότητα είναι ισοδύναμη με την από την οποία, λόγω της (), προκύπτει ότι: θ κ κ. θ. θ κ κ [7]
1ο Κεφάλαιο: Συστήματα
 ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
Άλγεβρα Β Λυκείου. Στέλιος Μιχαήλογλου.
 Άλγεβρα Β Λυκείου Στέλιος Μιχαήλογλου wwwaskisopolisgr Το φυλλάδιο αυτό δημιουργήθηκε για να χρησιμοποιηθεί ως επέκταση του σχολικού βιβλίου και όχι αυτόνομα δ έκδοση 0--06 Συστήματα Γραμμικές Εξισώσεις
Άλγεβρα Β Λυκείου Στέλιος Μιχαήλογλου wwwaskisopolisgr Το φυλλάδιο αυτό δημιουργήθηκε για να χρησιμοποιηθεί ως επέκταση του σχολικού βιβλίου και όχι αυτόνομα δ έκδοση 0--06 Συστήματα Γραμμικές Εξισώσεις
Άλγεβρα Β Λυκείου. Στέλιος Μιχαήλογλου.
 Άλγεβρα Β Λυκείου Στέλιος Μιχαήλογλου wwwaskisopolisgr Το φυλλάδιο αυτό δημιουργήθηκε για να χρησιμοποιηθεί ως επέκταση του σχολικού βιβλίου και όχι αυτόνομα δ έκδοση 0--06 Συστήματα Γραμμικές Εξισώσεις
Άλγεβρα Β Λυκείου Στέλιος Μιχαήλογλου wwwaskisopolisgr Το φυλλάδιο αυτό δημιουργήθηκε για να χρησιμοποιηθεί ως επέκταση του σχολικού βιβλίου και όχι αυτόνομα δ έκδοση 0--06 Συστήματα Γραμμικές Εξισώσεις
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου
 Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
2018 Φάση 2 ιαγωνίσµατα Επανάληψης ΑΛΓΕΒΡΑ. Β' Γενικού Λυκείου. Γενικής Παιδείας. Σάββατο 21 Απριλίου 2018 ιάρκεια Εξέτασης:3 ώρες ΘΕΜΑΤΑ
 ΘΕΜΑ A ΑΛΓΕΒΡΑ Β' Γενικού Λυκείου Γενικής Παιδείας Σάββατο 1 Απριλίου 018 ιάρκεια Εξέτασης: ώρες ΘΕΜΑΤΑ Α1. Στο επόμενο σχήμα βλέπετε τον τριγωνομετρικό κύκλο, τους άξονες ημιτόνων, συνημιτόνων, εφαπτομένων,
ΘΕΜΑ A ΑΛΓΕΒΡΑ Β' Γενικού Λυκείου Γενικής Παιδείας Σάββατο 1 Απριλίου 018 ιάρκεια Εξέτασης: ώρες ΘΕΜΑΤΑ Α1. Στο επόμενο σχήμα βλέπετε τον τριγωνομετρικό κύκλο, τους άξονες ημιτόνων, συνημιτόνων, εφαπτομένων,
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να αναγνωρίζει πότε μια αλγεβρική παράσταση της πραγματικής μεταβλητής x, είναι πολυώνυμο και να διακρίνει τα στοιχεία του: όροι, συντελεστές, σταθερός
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να αναγνωρίζει πότε μια αλγεβρική παράσταση της πραγματικής μεταβλητής x, είναι πολυώνυμο και να διακρίνει τα στοιχεία του: όροι, συντελεστές, σταθερός
ΑΛΓΕΒΡΑ B ΛΥΚΕΙΟΥ. Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ
 ΑΛΓΕΒΡΑ B ΛΥΚΕΙΥ Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΛΙΚΥ ΒΙΒΛΙΥ Σχολικό βιβλίο: Απαντήσεις Λύσεις Κεφάλαιο ο: Συστήματα Γραμμικά συστήματα Α ΜΑΔΑΣ Έχουμε: = 4 i = 6 = + = + = = Άρα, η λύση του συστήματος
ΑΛΓΕΒΡΑ B ΛΥΚΕΙΥ Γενικής Παιδείας ΑΠΑΝΤΗΣΕΙΣ ΛΥΣΕΙΣ ΣΧΛΙΚΥ ΒΙΒΛΙΥ Σχολικό βιβλίο: Απαντήσεις Λύσεις Κεφάλαιο ο: Συστήματα Γραμμικά συστήματα Α ΜΑΔΑΣ Έχουμε: = 4 i = 6 = + = + = = Άρα, η λύση του συστήματος
Κεφάλαιο 7 ο : Θετικοί και Αρνητικοί αριθμοί
 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΕΠΑΝΑΛΗΨΗ ΒΑΣΙΙΚΩΝ ΕΝΝΟΙΙΩΝ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Α ΤΑΞΗΣ Κεφάλαιο 7 ο : Θετικοί και Αρνητικοί αριθμοί Α. 7. 1 1. Τι είναι τα πρόσημα και πως χαρακτηρίζονται οι αριθμοί από αυτά; Τα σύμβολα
ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΕΠΑΝΑΛΗΨΗ ΒΑΣΙΙΚΩΝ ΕΝΝΟΙΙΩΝ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Α ΤΑΞΗΣ Κεφάλαιο 7 ο : Θετικοί και Αρνητικοί αριθμοί Α. 7. 1 1. Τι είναι τα πρόσημα και πως χαρακτηρίζονται οι αριθμοί από αυτά; Τα σύμβολα
2ογελ ΣΥΚΕΩΝ 2ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
K. Μυλωνάκης Αλγεβρα B Λυκείου
 ΠΟΛΥΩΝΥΜΑ Ονομάζουμε μονώνυμο του x κάθε πραγματικό αριθμό ή κάθε παράσταση της μορφής αx ν, όπου α είναι πραγμ. αριθμός και ν ένας θετικός ακέραιος. Π.χ. οι παραστάσεις 2χ 4, -3χ 2, 7 είναι μονώνυμα του
ΠΟΛΥΩΝΥΜΑ Ονομάζουμε μονώνυμο του x κάθε πραγματικό αριθμό ή κάθε παράσταση της μορφής αx ν, όπου α είναι πραγμ. αριθμός και ν ένας θετικός ακέραιος. Π.χ. οι παραστάσεις 2χ 4, -3χ 2, 7 είναι μονώνυμα του
ΔΑΜΙΑΝΟΣ ΓΙΑΝΝΗΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΛΛΟ ΕΠΑΝΑΛΗΨΗΣ 1
 ΘΕΜΑ Α ΦΥΛΛΟ 1 Α1. Να αποδείξετε ότι το υπόλοιπο υ της διαίρεσης ενός πολυωνύμου P(x) με το x - ρ είναι ίσο με την τιμή του πολυωνύμου για x = ρ. Είναι δηλαδή υ = P(ρ). Α. Να χαρακτηρίσετε τις προτάσεις
ΘΕΜΑ Α ΦΥΛΛΟ 1 Α1. Να αποδείξετε ότι το υπόλοιπο υ της διαίρεσης ενός πολυωνύμου P(x) με το x - ρ είναι ίσο με την τιμή του πολυωνύμου για x = ρ. Είναι δηλαδή υ = P(ρ). Α. Να χαρακτηρίσετε τις προτάσεις
1 ΘΕΩΡΙΑΣ...με απάντηση
 1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5
 Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5 Α Σύνολα αριθμών Για τα σύνολα των αριθμών γνωρίζουμε ότι N Z Q R. ) Το N= { 0,,,,... } είναι το σύνολο των φυσικών αριθμών. ) Το Z = { 0, ±, ±, ±,... } είναι το σύνολο
Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5 Α Σύνολα αριθμών Για τα σύνολα των αριθμών γνωρίζουμε ότι N Z Q R. ) Το N= { 0,,,,... } είναι το σύνολο των φυσικών αριθμών. ) Το Z = { 0, ±, ±, ±,... } είναι το σύνολο
9 Πολυώνυμα Διαίρεση πολυωνύμων
 4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις
 Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Μέτρηση του όγκου και του εμβαδού ορθών πρισμάτων Κανονική Πυραμίδα 1 Βάσης) (Απόστημα) 2 1 ό Βάσης) (Ύψος) 3
 Βασικά σύνολα αριθμών -Σύνολο φυσικών: Ν = {0,., } ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ -Σύνολο ακεραίων: Ζ= { -.-.0.,, } Συμβολίζουμε με ν=κ και τους άρτιους και τους περιττούς αντίστοιχα. * -Σύνολο ρητών: Q =, Z &
Βασικά σύνολα αριθμών -Σύνολο φυσικών: Ν = {0,., } ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ -Σύνολο ακεραίων: Ζ= { -.-.0.,, } Συμβολίζουμε με ν=κ και τους άρτιους και τους περιττούς αντίστοιχα. * -Σύνολο ρητών: Q =, Z &
ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ
 ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Άσκηση η Γραμμικά συστήματα Δίνονται οι ευθείες : y3 και :y 5. Να βρεθεί το R, ώστε οι ευθείες να τέμνονται. Οι ευθείες και θα τέμνονται όταν το μεταξύ
ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Άσκηση η Γραμμικά συστήματα Δίνονται οι ευθείες : y3 και :y 5. Να βρεθεί το R, ώστε οι ευθείες να τέμνονται. Οι ευθείες και θα τέμνονται όταν το μεταξύ
Bbs. ΑΛΓΕΒΡΑ ΣΥΝΟΛΑ Σύνολο Φυσικών αριθμών: N = {0,1,2, } Σύνολο Ακέραιων αριθμών: Z = {,-2,-1,0,1,2, } Σύνολο Ρητών αριθμών: Q = {
 ΑΛΓΕΒΡΑ ΣΥΝΟΛΑ Σύνολο Φυσικών αριθμών: N = {0,1,2, } Σύνολο Ακέραιων αριθμών: Z = {,-2,-1,0,1,2, } Σύνολο Ρητών αριθμών: Q = { Άρρητοι αριθμοί A: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών αριθμών R=
ΑΛΓΕΒΡΑ ΣΥΝΟΛΑ Σύνολο Φυσικών αριθμών: N = {0,1,2, } Σύνολο Ακέραιων αριθμών: Z = {,-2,-1,0,1,2, } Σύνολο Ρητών αριθμών: Q = { Άρρητοι αριθμοί A: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών αριθμών R=
ΕΠΑΝΑΛΗΨΗ ΤΡΙΓΩΝΟΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ
 ΚΕΦΑΛΑΙΟ Ο ΕΠΑΝΑΛΗΨΗ ΤΡΙΓΩΝΟΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ Το ακτίνιο ως μονάδα μέτρησης γωνιών: Το ακτίνιο (ή rad) είναι η γωνία που, όταν γίνει επίκεντρη κύκλου (Ο, ρ), βαίνει σε τόξο που έχει μήκος ίσο με την ακτίνα
ΚΕΦΑΛΑΙΟ Ο ΕΠΑΝΑΛΗΨΗ ΤΡΙΓΩΝΟΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ Το ακτίνιο ως μονάδα μέτρησης γωνιών: Το ακτίνιο (ή rad) είναι η γωνία που, όταν γίνει επίκεντρη κύκλου (Ο, ρ), βαίνει σε τόξο που έχει μήκος ίσο με την ακτίνα
1.0 Βασικές Έννοιες στην Τριγωνομετρία
 .0 Βασικές Έννοιες στην Τριγωνομετρία Εύρεση τριγωνομετρικών αριθμών οξείας γωνίας σε ορθογώνιο τρίγωνο. ΑΠΑΝΤΗΣΗ Έστω ορθογώνιο τρίγωνο ΑΒΓ (Α= 90 0 ). Οι τριγωνομετρικοί αριθμοί μιας οξείας γωνίας ορίζονται
.0 Βασικές Έννοιες στην Τριγωνομετρία Εύρεση τριγωνομετρικών αριθμών οξείας γωνίας σε ορθογώνιο τρίγωνο. ΑΠΑΝΤΗΣΗ Έστω ορθογώνιο τρίγωνο ΑΒΓ (Α= 90 0 ). Οι τριγωνομετρικοί αριθμοί μιας οξείας γωνίας ορίζονται
ΜΑΘΗΜΑΤΙΚΟ ΤΥΠΟΛΟΓΙΟ Α - Β ΛΥΚΕΙΟΥ 1. ΣΥΝΟΛΑ ΑΡΙΘΜΩΝ
 1. ΣΥΝΟΛΑ ΑΡΙΘΜΩΝ 1. Φυσικοί αριθμοί : Ν = {0,1,,3,4,...}. Ακέραιοι αριθμοί : Ζ = {...-4,-3,-,-1,0,1,,3,4,...} 3. Ρητοί αριθμοί : Q = { ì í, μ Ζ, ν Ζ* } Σημ. Το σύνολο Q των ρητών αριθμών ταυτίζεται με
1. ΣΥΝΟΛΑ ΑΡΙΘΜΩΝ 1. Φυσικοί αριθμοί : Ν = {0,1,,3,4,...}. Ακέραιοι αριθμοί : Ζ = {...-4,-3,-,-1,0,1,,3,4,...} 3. Ρητοί αριθμοί : Q = { ì í, μ Ζ, ν Ζ* } Σημ. Το σύνολο Q των ρητών αριθμών ταυτίζεται με
1.1 ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ 1.2 ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Να γίνουν οι γραφικές παραστάσεις των συναρτήσεων : π α) f() = + ηµ β) g() = + συν( ) 6 π π γ) f() = ηµ( ) δ) g() = συν( ) Να γίνει η µελέτη και η γραφική παράσταση
ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Να γίνουν οι γραφικές παραστάσεις των συναρτήσεων : π α) f() = + ηµ β) g() = + συν( ) 6 π π γ) f() = ηµ( ) δ) g() = συν( ) Να γίνει η µελέτη και η γραφική παράσταση
ΑΛΓΕΒΡΑ Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 ΑΛΓΕΒΡΑ Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΤΟΙΧΕΙΑ ΑΡΧΙΚΗΣ ΕΚ ΟΣΗΣ Συγγραφική ομάδα: Ανδρεαδάκης Στυλιανός Κατσαργύρης Βασίλειος Παπασταυρίδης Σταύρος Πολύζος Γεώργιος Σβέρκος Ανδρέας Καθηγητής Πανεπιστημίου Αθηνών Καθηγητής
ΑΛΓΕΒΡΑ Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΤΟΙΧΕΙΑ ΑΡΧΙΚΗΣ ΕΚ ΟΣΗΣ Συγγραφική ομάδα: Ανδρεαδάκης Στυλιανός Κατσαργύρης Βασίλειος Παπασταυρίδης Σταύρος Πολύζος Γεώργιος Σβέρκος Ανδρέας Καθηγητής Πανεπιστημίου Αθηνών Καθηγητής
1 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ 2008
 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ 008 α). Να αποδείξετε ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου Ρ(x) με το πρωτοβάθμιο πολυώνυμο x ρ ισούται με την αριθμητική τιμή του Ρ(x) για x =
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ 008 α). Να αποδείξετε ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου Ρ(x) με το πρωτοβάθμιο πολυώνυμο x ρ ισούται με την αριθμητική τιμή του Ρ(x) για x =
Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ Πραγματική Συνάρτηση ρισμός Έστω Α ένα υποσύνολο του R. νομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο
Ε π ι μ έ λ ε ι α Κ Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ Πραγματική Συνάρτηση ρισμός Έστω Α ένα υποσύνολο του R. νομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο
ΓΥΜΝΑΣΙΟ ΚΑΣΤΕΛΛΑΝΩΝ ΜΕΣΗΣ ΑΛΓΕΒΡΑ
 ΑΛΓΕΒΡΑ ΠΡΟΑΠΑΙΤΟΥΜΕΝΑ ΑΠΟ Α ΓΥΜΝΑΣΙΟΥ Ομόσημοι Ετερόσημοι αριθμοί Αντίθετοι Αντίστροφοι αριθμοί Πρόσθεση ομόσημων και ετερόσημων ρητών αριθμών Απαλοιφή παρενθέσεων Πολλαπλασιασμός και Διαίρεση ρητών αριθμών
ΑΛΓΕΒΡΑ ΠΡΟΑΠΑΙΤΟΥΜΕΝΑ ΑΠΟ Α ΓΥΜΝΑΣΙΟΥ Ομόσημοι Ετερόσημοι αριθμοί Αντίθετοι Αντίστροφοι αριθμοί Πρόσθεση ομόσημων και ετερόσημων ρητών αριθμών Απαλοιφή παρενθέσεων Πολλαπλασιασμός και Διαίρεση ρητών αριθμών
Θέματα ενδοσχολικών εξετάσεων Άλγεβρας Β Λυκείου Σχ. έτος , Ν. Δωδεκανήσου ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 2013-2014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών Μαθηματικός Περιηγητής 1 ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων
ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 2013-2014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών Μαθηματικός Περιηγητής 1 ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων
ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ
 ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό σας. ΚΕΦΑΛΑΙΟ 1 1. Να συμπληρώσετε
ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό σας. ΚΕΦΑΛΑΙΟ 1 1. Να συμπληρώσετε
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
 ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ Τελευταία ενηµέρωση: Νοέµβριος 016) Ανέστης Τσοµίδης Κατερίνη Περιεχόµενα 1 Συστήµατα 1.1 Μη γραµµικά συστήµατα........................ Ιδιότητες συναρτήσεων 3.1 Μονοτονία,
ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ Τελευταία ενηµέρωση: Νοέµβριος 016) Ανέστης Τσοµίδης Κατερίνη Περιεχόµενα 1 Συστήµατα 1.1 Μη γραµµικά συστήµατα........................ Ιδιότητες συναρτήσεων 3.1 Μονοτονία,
ΕΠΑΝΑΛΗΨΗ Α ΓΥΜΝΑΣΙΟΥ
 ΕΠΑΝΑΛΗΨΗ Α ΓΥΜΝΑΣΙΟΥ ΘΕΩΡΙΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ Α.1. 1) Ποιοι φυσικοί αριθμοί λέγονται άρτιοι και ποιοι περιττοί; ( σ. 11 ) 2) Από τι καθορίζεται η αξία ενός ψηφίου σ έναν φυσικό αριθμό; ( σ. 11 ) 3) Τι
ΕΠΑΝΑΛΗΨΗ Α ΓΥΜΝΑΣΙΟΥ ΘΕΩΡΙΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ Α.1. 1) Ποιοι φυσικοί αριθμοί λέγονται άρτιοι και ποιοι περιττοί; ( σ. 11 ) 2) Από τι καθορίζεται η αξία ενός ψηφίου σ έναν φυσικό αριθμό; ( σ. 11 ) 3) Τι
Πολυωνυμική εξίσωση βαθμού ν ονομάζεται κάθε εξίσωση της μορφής α ν x ν +α ν-1 x ν α 1 x+α 0 =0,με α 0,α 1,...
 3 0 ΛΥΚΕΙΟ ΚΕΡΑΤΣΙΝΙΟΥ Λ. ΒΟΥΛΓΑΡΗ ΜΑΘΗΜΑΤΙΚΟΣ ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΕΞΙΣΩΣΕΙΣ ΠΟΥ ΑΝΑΓΟΝΤΑΙ ΣΕ ΠΟΛΥΩΝΥΜΙΚΕΣ Πολυωνυμική εξίσωση βαθμού ν ονομάζεται κάθε εξίσωση της μορφής α ν x ν +α ν-1 x ν-1 +...+α
3 0 ΛΥΚΕΙΟ ΚΕΡΑΤΣΙΝΙΟΥ Λ. ΒΟΥΛΓΑΡΗ ΜΑΘΗΜΑΤΙΚΟΣ ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΕΞΙΣΩΣΕΙΣ ΠΟΥ ΑΝΑΓΟΝΤΑΙ ΣΕ ΠΟΛΥΩΝΥΜΙΚΕΣ Πολυωνυμική εξίσωση βαθμού ν ονομάζεται κάθε εξίσωση της μορφής α ν x ν +α ν-1 x ν-1 +...+α
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Α Λ Γ Ε Β Ρ Α Β Λ Υ Κ Ε Ι Ο Υ. ΚΕΦΑΛΑΙΟ 4 ο ΠΟΛΥΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 Α Λ Γ Ε Β Ρ Α Β Λ Υ Κ Ε Ι Ο Υ ΚΕΦΑΛΑΙΟ 4 ο ΠΟΛΥΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Συνοπτική Θεωρία Ασκήσεις της Τράπεζας Θεμάτων Ερωτήσεις Σωστού-Λάθους Διαγωνίσματα Επιμέλεια: Συντακτική ομάδα mathp.gr Συντονισμός
Α Λ Γ Ε Β Ρ Α Β Λ Υ Κ Ε Ι Ο Υ ΚΕΦΑΛΑΙΟ 4 ο ΠΟΛΥΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Συνοπτική Θεωρία Ασκήσεις της Τράπεζας Θεμάτων Ερωτήσεις Σωστού-Λάθους Διαγωνίσματα Επιμέλεια: Συντακτική ομάδα mathp.gr Συντονισμός
4.1. Πολυώνυμα. Η έννοια του πολυωνύμου
 4.1 Πολυώνυμα Η έννοια του πολυωνύμου ΟΡΙΣΜΟΙ 1. Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής αx ν, όπου α R, ν N (σταθερές) και x R (μεταβλητή).. Πολυώνυμο του x ονομάζουμε κάθε παράσταση της μορφής:
4.1 Πολυώνυμα Η έννοια του πολυωνύμου ΟΡΙΣΜΟΙ 1. Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής αx ν, όπου α R, ν N (σταθερές) και x R (μεταβλητή).. Πολυώνυμο του x ονομάζουμε κάθε παράσταση της μορφής:
Α ΜΕΡΟΣ - ΑΛΓΕΒΡΑ. Α. Οι πραγματικοί αριθμοί και οι πράξεις τους
 Α ΜΕΡΟΣ - ΑΛΓΕΒΡΑ Κεφάλαιο 1 ο ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ 1.1 Πράξεις με πραγματικούς αριθμούς Α. Οι πραγματικοί αριθμοί και οι πράξεις τους 1. Ποιοι αριθμοί ονομάζονται: α) ρητοί β) άρρητοι γ) πραγματικοί;
Α ΜΕΡΟΣ - ΑΛΓΕΒΡΑ Κεφάλαιο 1 ο ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ 1.1 Πράξεις με πραγματικούς αριθμούς Α. Οι πραγματικοί αριθμοί και οι πράξεις τους 1. Ποιοι αριθμοί ονομάζονται: α) ρητοί β) άρρητοι γ) πραγματικοί;
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Ταυτότητες. α 2 β 2 = (α β)(α + β) "διαφορά τετραγώνων" α 3 β 3 = (α β)(α 2 + αβ + β 2 ) "διαφορά κύβων"
 Ταυτότητες (α β) α αβ β " αναπτύγματα τετραγώνων " (α β) αβ β (α β) α α β αβ β " αναπτύγματα κύβων " (α β) α α β αβ β " παραγοντοποίηση τριωνύμου " (α β) αβ ( α)( β) (α β) αβ ( α)( β) α β = (α β)(α + β)
Ταυτότητες (α β) α αβ β " αναπτύγματα τετραγώνων " (α β) αβ β (α β) α α β αβ β " αναπτύγματα κύβων " (α β) α α β αβ β " παραγοντοποίηση τριωνύμου " (α β) αβ ( α)( β) (α β) αβ ( α)( β) α β = (α β)(α + β)
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ 1 ο : Όριο Συνέχεια Συνάρτησης
 ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία
ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ
 ΤΥΠΛΓΙ ΜΑΘΗΜΑΤΙΚΩΝ Βασικά σύνολα Σύνολο φυσικών: Í {,,,L} Σύνολο ακεραίων: Æ { L,,,,,, L} Σύνολο ρητών: Q / Æ, ë Æ * ë Άρρητος λέγεται ένας αριθµός που δεν µπορεί να γραφτεί µε τη µορφή κλάσµατος ακεραίων.
ΤΥΠΛΓΙ ΜΑΘΗΜΑΤΙΚΩΝ Βασικά σύνολα Σύνολο φυσικών: Í {,,,L} Σύνολο ακεραίων: Æ { L,,,,,, L} Σύνολο ρητών: Q / Æ, ë Æ * ë Άρρητος λέγεται ένας αριθµός που δεν µπορεί να γραφτεί µε τη µορφή κλάσµατος ακεραίων.
ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ. f : A R και στη συνέχεια δίνουμε τον τύπο της συνάρτησης, π.χ.
 Συναρτήσεις σελ ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα),
Συναρτήσεις σελ ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα),
4.1. Πολυώνυμα. Η έννοια του πολυωνύμου
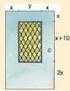 4.1 Πολυώνυμα Η έννοια του πολυωνύμου ΟΡΙΣΜΟΙ 1. Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής αx ν, όπου α R, ν N (σταθερές) και x R (μεταβλητή). 2. Πολυώνυμο του x ονομάζουμε κάθε παράσταση της
4.1 Πολυώνυμα Η έννοια του πολυωνύμου ΟΡΙΣΜΟΙ 1. Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής αx ν, όπου α R, ν N (σταθερές) και x R (μεταβλητή). 2. Πολυώνυμο του x ονομάζουμε κάθε παράσταση της
Web page: Συνοπτική Θεωρία Μαθηματικών Γ Γυμνασίου Γεωμετρία-Τριγωνομετρία
 Web page: www.ma8eno.gr e-mail: vrentzou@ma8eno.gr Η αποτελεσματική μάθηση δεν θέλει κόπο αλλά τρόπο, δηλαδή ma8eno.gr Άλγεβρα Κανόνας των πρόσημων: (+) (+) = + ( ) ( ) = + (+) ( ) = ( ) (+) = Συνοπτική
Web page: www.ma8eno.gr e-mail: vrentzou@ma8eno.gr Η αποτελεσματική μάθηση δεν θέλει κόπο αλλά τρόπο, δηλαδή ma8eno.gr Άλγεβρα Κανόνας των πρόσημων: (+) (+) = + ( ) ( ) = + (+) ( ) = ( ) (+) = Συνοπτική
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΜΗ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΥΝΑΡΤΗΣΕΙΣ ΜΟΝΟΤΟΝΙΑ-ΑΚΡΟΤΑΤΑ-ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ
 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4_095. Δίνονται οι ευθείες ε 1: λx + y = 1 και ε : x + λy = λ α) Να βρείτε για ποιες τιμές του λ οι δύο ευθείες τέμνονται και να γράψετε τις συντεταγμένες του κοινού τους σημείου συναρτήσει
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4_095. Δίνονται οι ευθείες ε 1: λx + y = 1 και ε : x + λy = λ α) Να βρείτε για ποιες τιμές του λ οι δύο ευθείες τέμνονται και να γράψετε τις συντεταγμένες του κοινού τους σημείου συναρτήσει
ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ ΙΟΥΝΙΟΥ ΑΛΓΕΒΡΑ Β 2016
 ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ ΙΟΥΝΙΟΥ ΑΛΓΕΒΡΑ Β 06 version -6-06 Παρακάτω υπάρχουν θέματα θεωρίας και ασκήσεις που καλύπτουν πιστεύω σε μεγάλο βαθμό την εξεταστέα ύλη. Εχουν στόχο να μας βοηθήσουν να θυμηθούμε την
ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ ΙΟΥΝΙΟΥ ΑΛΓΕΒΡΑ Β 06 version -6-06 Παρακάτω υπάρχουν θέματα θεωρίας και ασκήσεις που καλύπτουν πιστεύω σε μεγάλο βαθμό την εξεταστέα ύλη. Εχουν στόχο να μας βοηθήσουν να θυμηθούμε την
τα βιβλία των επιτυχιών
 Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
II. Συναρτήσεις. math-gr
 II Συναρτήσεις Παντελής Μπουμπούλης, MSc, PhD σελ blogspotcom, bouboulismyschgr ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική
II Συναρτήσεις Παντελής Μπουμπούλης, MSc, PhD σελ blogspotcom, bouboulismyschgr ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική
Επαναληπτικές Ασκήσεις
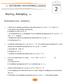 Επαναληπτικές Ασκήσεις Έστω ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου ( x ) α Να γράψετε την ταυτότητα της διαίρεσης β Να βρείτε τα 0 και Ρ γ Αν το πολυώνυμο ( x) είναι x να βρείτε: x + x είναι 3x
Επαναληπτικές Ασκήσεις Έστω ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου ( x ) α Να γράψετε την ταυτότητα της διαίρεσης β Να βρείτε τα 0 και Ρ γ Αν το πολυώνυμο ( x) είναι x να βρείτε: x + x είναι 3x
ΝΙΚΟΣ ΤΑΣΟΣ. Αλγ ε β ρ α. Γενικής Παιδειασ
 ΝΙΚΟΣ ΤΑΣΟΣ Αλγ ε β ρ α Β Λυ κ ε ί ο υ Γενικής Παιδειασ Α Τό μ ο ς 3η Εκ δ ο σ η Πρόλογος Το βιβλίο αυτό έχει σκοπό και στόχο αφενός μεν να βοηθήσει τους μαθητές της Β Λυκείου να κατανοήσουν καλύτερα την
ΝΙΚΟΣ ΤΑΣΟΣ Αλγ ε β ρ α Β Λυ κ ε ί ο υ Γενικής Παιδειασ Α Τό μ ο ς 3η Εκ δ ο σ η Πρόλογος Το βιβλίο αυτό έχει σκοπό και στόχο αφενός μεν να βοηθήσει τους μαθητές της Β Λυκείου να κατανοήσουν καλύτερα την
Γιώργος Μπαρακλιανός τηλ ( ) Κώστας Τζάλλας τηλ ( ) Παραγγελίες : τηλ.
 Γιώργος Μπαρακλιανός τηλ. 69377886 ( mparakgeo@gmail.com ) Κώστας Τζάλλας τηλ. 69733004 ( tzallask@gmail.com ) Παραγγελίες : τηλ. 5407604 Email : mparakgeo@gmail.com Messenger : Giorgos Mparaklianos Πρόλογος
Γιώργος Μπαρακλιανός τηλ. 69377886 ( mparakgeo@gmail.com ) Κώστας Τζάλλας τηλ. 69733004 ( tzallask@gmail.com ) Παραγγελίες : τηλ. 5407604 Email : mparakgeo@gmail.com Messenger : Giorgos Mparaklianos Πρόλογος
Συναρτήσεις Όρια Συνέχεια
 Κωνσταντίνος Παπασταματίου Μαθηματικά Γ Λυκείου Κατεύθυνσης Συναρτήσεις Όρια Συνέχεια Συνοπτική Θεωρία Μεθοδολογίες Λυμένα Παραδείγματα Επιμέλεια: Μαθηματικός Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με
Κωνσταντίνος Παπασταματίου Μαθηματικά Γ Λυκείου Κατεύθυνσης Συναρτήσεις Όρια Συνέχεια Συνοπτική Θεωρία Μεθοδολογίες Λυμένα Παραδείγματα Επιμέλεια: Μαθηματικός Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 (με
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να
Α ΛΥΚΕΙΟ ΓΕΡΑΚΑ. ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Σχολικό Έτος ΜΑΝΩΛΗ ΨΑΡΡΑ. Μανώλης Ψαρράς Σελίδα 1
 Α ΛΥΚΕΙΟ ΓΕΡΑΚΑ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Σχολικό Έτος 014-15 ΜΑΝΩΛΗ ΨΑΡΡΑ Μανώλης Ψαρράς Σελίδα 1 Α ΣΥΣΤΗΜΑΤΑ ΑΣΚΗΣΗ 1 η Να λυθούν γραφικά τα συστήματα: y y6 y 5 1 : 1 : 3 : y 6 0 y 5
Α ΛΥΚΕΙΟ ΓΕΡΑΚΑ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Σχολικό Έτος 014-15 ΜΑΝΩΛΗ ΨΑΡΡΑ Μανώλης Ψαρράς Σελίδα 1 Α ΣΥΣΤΗΜΑΤΑ ΑΣΚΗΣΗ 1 η Να λυθούν γραφικά τα συστήματα: y y6 y 5 1 : 1 : 3 : y 6 0 y 5
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου
 Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
1. ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΕΝΝΟΙΕΣ ΑΝΑΓΩΓΗ ΣΤΟ 1 Ο ΤΕΤΑΡΤΗΜΟΡΙΟ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ
 1. ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΕΝΝΟΙΕΣ ΑΝΑΓΩΓΗ ΣΤΟ 1 Ο ΤΕΤΑΡΤΗΜΟΡΙΟ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ Έστω ΑΒΓ ένα ορθογώνιο τρίγωνο Είναι γνωστό ότι: ( ΑΒ) ηµ Γ= ( ΒΓ ) ( ΑΓ) συν Γ= ( ΒΓ ) ( ΑΒ) εφ Γ= ( ΑΓ ) ( ΑΓ)
1. ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΕΝΝΟΙΕΣ ΑΝΑΓΩΓΗ ΣΤΟ 1 Ο ΤΕΤΑΡΤΗΜΟΡΙΟ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ Έστω ΑΒΓ ένα ορθογώνιο τρίγωνο Είναι γνωστό ότι: ( ΑΒ) ηµ Γ= ( ΒΓ ) ( ΑΓ) συν Γ= ( ΒΓ ) ( ΑΒ) εφ Γ= ( ΑΓ ) ( ΑΓ)
1 of 79 ΘΕΜΑ 2. Δίνεται η συνάρτηση f(x) = x 2 4x + 5, x R
 1 of 79 Δίνεται η συνάρτηση f(x) = x 2 4x + 5, x R α) Να αποδείξετε ότι η f γράφεται στη μορφή f(x) = (x- 2) 2 + 1. (Μονάδες 12) β) Στο σύστημα συντεταγμένων που ακολουθεί, να παραστήσετε γραφικά τη συνάρτηση
1 of 79 Δίνεται η συνάρτηση f(x) = x 2 4x + 5, x R α) Να αποδείξετε ότι η f γράφεται στη μορφή f(x) = (x- 2) 2 + 1. (Μονάδες 12) β) Στο σύστημα συντεταγμένων που ακολουθεί, να παραστήσετε γραφικά τη συνάρτηση
ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΜΑΘΗΜΑΤΙΚΟΣ
 qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj klzxcvλοπbnαmqwertyuiopasdfghjklz ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ
qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj klzxcvλοπbnαmqwertyuiopasdfghjklz ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
 ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ Οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς, τους φυσικούς και τους ακέραιους αριθμούς. Δηλαδή είναι το μεγαλύτερο σύνολο αριθμών που μπορούμε
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ Οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς, τους φυσικούς και τους ακέραιους αριθμούς. Δηλαδή είναι το μεγαλύτερο σύνολο αριθμών που μπορούμε
ΚΕΦΑΛΑΙΟ 3 ο ΘΕΩΡΙΑ. 3.1 Τριγωνομετρικοί Αριθμοί Γωνίας
 ΚΕΦΑΛΑΙΟ 3 ο ΘΕΩΡΙΑ Τριγωνομετρικοί αριθμοί οξείας γωνίας Δίνεται ορθογώνιο τρίγωνο ΑΒΓ, με Α = 90 ο, κάθετες πλευρές β, γ και οξεία γωνία ω. απέναντι κάθετη Ορίζουμε, ημω = υποτείνουσα συνω = προσκείμενη
ΚΕΦΑΛΑΙΟ 3 ο ΘΕΩΡΙΑ Τριγωνομετρικοί αριθμοί οξείας γωνίας Δίνεται ορθογώνιο τρίγωνο ΑΒΓ, με Α = 90 ο, κάθετες πλευρές β, γ και οξεία γωνία ω. απέναντι κάθετη Ορίζουμε, ημω = υποτείνουσα συνω = προσκείμενη
Τ ρ α π ε ζ α Θ ε μ α τ ω ν
 Τ ρ α π ε ζ α Θ ε μ α τ ω ν Α λ γ ε β ρ α B Λ υ κ ε ι ο υ Ε π ι μ ε λ ε ι α : Τ α κ η ς Τ σ α κ α λ α κ ο ς Α λ γ ε β ρ α B Λ υ κ ε ι ο υ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Γ ρ α μ μ ι κ α Σ υ σ τ η μ α τ α 16950 16954
Τ ρ α π ε ζ α Θ ε μ α τ ω ν Α λ γ ε β ρ α B Λ υ κ ε ι ο υ Ε π ι μ ε λ ε ι α : Τ α κ η ς Τ σ α κ α λ α κ ο ς Α λ γ ε β ρ α B Λ υ κ ε ι ο υ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Γ ρ α μ μ ι κ α Σ υ σ τ η μ α τ α 16950 16954
Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις
 2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Β ΤΑΞΗΣ ΜΕΡΟΣ Α -- ΑΛΓΕΒΡΑ Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις Α. 1 1 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση
2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Β ΤΑΞΗΣ ΜΕΡΟΣ Α -- ΑΛΓΕΒΡΑ Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις Α. 1 1 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση
( ) ( ) Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή x. αντικ σταση στο που = α. [ ο αριθµ ός πουτο µηδεν ίζει
 μέρος πρώτο v v 1 v 1 Γενική μορφή πολυωνύμου: ( ) 1 1 Όροι του ( ) v v v P = a v + av 1 + av +... + a + a 1 + a, ν Ν, α ν R Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή. P : a, a, a,...,
μέρος πρώτο v v 1 v 1 Γενική μορφή πολυωνύμου: ( ) 1 1 Όροι του ( ) v v v P = a v + av 1 + av +... + a + a 1 + a, ν Ν, α ν R Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή. P : a, a, a,...,
ProapaitoÔmenec gn seic.
 ProapaitoÔmeec g seic. Α. Το σύνολο των πραγματικών αριθμών R και οι αλγεβρικές ιδιότητες των τεσσάρων πράξεων στο R. Το σύνολο των φυσικών αριθμών N = {1,, 3,... }. Προσέξτε: μερικά βιβλία (τα βιβλία
ProapaitoÔmeec g seic. Α. Το σύνολο των πραγματικών αριθμών R και οι αλγεβρικές ιδιότητες των τεσσάρων πράξεων στο R. Το σύνολο των φυσικών αριθμών N = {1,, 3,... }. Προσέξτε: μερικά βιβλία (τα βιβλία
Ρητοί αριθμοί λέγονται οι αριθμοί που έχουν ή μπορούν να πάρουν τη μορφή
 ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ)-ΘΕΩΡΕΙΑ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμώv αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ)-ΘΕΩΡΕΙΑ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμώv αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj
 qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ klzxcvλοπbnαmqwertyuiopasdfghjklz
qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ klzxcvλοπbnαmqwertyuiopasdfghjklz
Άλγεβρα Β Λυκείου Επαναληπτικά θέματα ΟΕΦΕ α φάση
 Άλγεβρα Β Λυκείου Επαναληπτικά θέματα ΟΕΦΕ 00-08 α φάση Συναρτήσεις Θεωρούμε τη συνάρτηση Α, 6 wwwaskisopolisgr f κ, με 4,4 και κ η οποία διέρχεται από το σημείο και τμήμα της γραφικής της παράστασης φαίνεται
Άλγεβρα Β Λυκείου Επαναληπτικά θέματα ΟΕΦΕ 00-08 α φάση Συναρτήσεις Θεωρούμε τη συνάρτηση Α, 6 wwwaskisopolisgr f κ, με 4,4 και κ η οποία διέρχεται από το σημείο και τμήμα της γραφικής της παράστασης φαίνεται
Φίλη μαθήτρια, φίλε μαθητή,
 Φίλη μαθήτρια φίλε μαθητή Η εργασία αυτή έγινε με σκοπό να συμβάλει στην κατανόηση στην εμπέδωση και στην εμβάθυνση των μαθηματικών εννοιών που αναπτύσσονται στην Άλγεβρα της Β Λυκείου. Η ύλη είναι γραμμένη
Φίλη μαθήτρια φίλε μαθητή Η εργασία αυτή έγινε με σκοπό να συμβάλει στην κατανόηση στην εμπέδωση και στην εμβάθυνση των μαθηματικών εννοιών που αναπτύσσονται στην Άλγεβρα της Β Λυκείου. Η ύλη είναι γραμμένη
Ιωάννης Σ. Μιχέλης Μαθηματικός
 1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται αριθμητική και τι αλγεβρική παράσταση; Μία παράσταση, που περιέχει πράξεις με αριθμούς ονομάζεται αριθμητική παράσταση. Μία παράσταση, που περιέχει πράξεις
1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται αριθμητική και τι αλγεβρική παράσταση; Μία παράσταση, που περιέχει πράξεις με αριθμούς ονομάζεται αριθμητική παράσταση. Μία παράσταση, που περιέχει πράξεις
Μαθηματικά Β Γυμνασίου
 Μαθηματικά Β Γυμνασίου Περιεχόμενα KEΦΑΛΑΙΟ 1 ΕΞΙΣΩΣΕΙΣ... 3 1.1 Η ΕΝΝΟΙΑ ΤΗΣ ΜΕΤΑΒΛΗΤΗΣ ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ... 3 1.2 ΕΞΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ... 3 1.3 ΕΠΙΛΥΣΗ ΤΥΠΩΝ... 4 1.4 ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΜΕ ΤΗΝ ΧΡΗΣΗ
Μαθηματικά Β Γυμνασίου Περιεχόμενα KEΦΑΛΑΙΟ 1 ΕΞΙΣΩΣΕΙΣ... 3 1.1 Η ΕΝΝΟΙΑ ΤΗΣ ΜΕΤΑΒΛΗΤΗΣ ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ... 3 1.2 ΕΞΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ... 3 1.3 ΕΠΙΛΥΣΗ ΤΥΠΩΝ... 4 1.4 ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΜΕ ΤΗΝ ΧΡΗΣΗ
β) Αν επιπλέον το υπόλοιπο της διαίρεσης είναι υ(x) = - 3x + 5, τότε να βρείτε το Δ(x). (Απ. α) 5 ος β) Δ(x) = x 5 5x 4 + 6x 3 + 4x 2 11x + 5)
 ΠΑΝΤΕΛΗΣ ΤΡΙΜΗΣ ΜΑΘΗΜΑΤΙΚΟΣ ΑΛΓΕΒΡΑ B Λυκείου Γενικής Παιδείας Κ Ε Φ Α Λ Α Ι Ο 4ο - Φ Υ Λ Λ Ο Νο 2 Δ Ι Α Ι Ρ Ε Σ Η ΠΟΛΥΩΝΥΜΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΟΛΥΩΝΥΜΙΚΕΣ ΑΝΙΣΩΣΕΙΣ ΑΣΚΗΣΕΙΣ 1. Ένα πολυώνυμο Δ(x),
ΠΑΝΤΕΛΗΣ ΤΡΙΜΗΣ ΜΑΘΗΜΑΤΙΚΟΣ ΑΛΓΕΒΡΑ B Λυκείου Γενικής Παιδείας Κ Ε Φ Α Λ Α Ι Ο 4ο - Φ Υ Λ Λ Ο Νο 2 Δ Ι Α Ι Ρ Ε Σ Η ΠΟΛΥΩΝΥΜΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΟΛΥΩΝΥΜΙΚΕΣ ΑΝΙΣΩΣΕΙΣ ΑΣΚΗΣΕΙΣ 1. Ένα πολυώνυμο Δ(x),
qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj
 qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ klzxcvλοπbnαmqwertyuiopasdfghjklz
qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ klzxcvλοπbnαmqwertyuiopasdfghjklz
7. Αν υψώσουμε και τα δύο μέλη μιας εξίσωσης στον κύβο (και γενικά σε οποιαδήποτε περιττή δύναμη), τότε προκύπτει
 8 7y = 4 y + y ( 8 7y) = ( 4 y + y) ( y) + 4 y y 4 y = 4 y y 8 7y = 4 y + ( 4 y) = ( 4 y y) ( 4 y) = 4( 4 y)( y) ( 4 y) 4( 4 y)( y) = 0 ( 4 y) [ 4 y 4( y) ] = 4 ( 4 y)( y + 4) = 0 y = ή y = 4) 0 4 H y
8 7y = 4 y + y ( 8 7y) = ( 4 y + y) ( y) + 4 y y 4 y = 4 y y 8 7y = 4 y + ( 4 y) = ( 4 y y) ( 4 y) = 4( 4 y)( y) ( 4 y) 4( 4 y)( y) = 0 ( 4 y) [ 4 y 4( y) ] = 4 ( 4 y)( y + 4) = 0 y = ή y = 4) 0 4 H y
ΣΤΟΙΧΕΙΑ ΑΡΧΙΚΗΣ ΕΚ ΟΣΗΣ
 ΣΤΟΙΧΕΙΑ ΑΡΧΙΚΗΣ ΕΚ ΟΣΗΣ Συγγραφική ομάδα: Ανδρεαδάκης Στυλιανός Κατσαργύρης Βασίλειος Παπασταυρίδης Σταύρος Πολύζος Γεώργιος Σβέρκος Ανδρέας Καθηγητής Πανεπιστημίου Αθηνών Καθηγητής μαθηματικών Βαρβακείου
ΣΤΟΙΧΕΙΑ ΑΡΧΙΚΗΣ ΕΚ ΟΣΗΣ Συγγραφική ομάδα: Ανδρεαδάκης Στυλιανός Κατσαργύρης Βασίλειος Παπασταυρίδης Σταύρος Πολύζος Γεώργιος Σβέρκος Ανδρέας Καθηγητής Πανεπιστημίου Αθηνών Καθηγητής μαθηματικών Βαρβακείου
Px α x α x... α x α. Ο αριθμός κ λέγεται βαθμός
 ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΑΛΓΕΒΡΑ ΘΕΜΑ Α Α1. Να δείξετε ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου Px με το x ρ είναι ίσο με την τιμή του πολυωνύμου για
ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΑΛΓΕΒΡΑ ΘΕΜΑ Α Α1. Να δείξετε ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου Px με το x ρ είναι ίσο με την τιμή του πολυωνύμου για
ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
 ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του
ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του
ΘΕΜΑ Α ΘΕΜΑ B. Β.1. Γνωρίζουμε ότι τα σημεία Α(π,4) και Β(-2π,6) ανήκουν στην ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ
 ΘΕΜΑ Α Α.1. Η απόδειξη βρίσκεται στη σελίδα 175 του σχολικού βιβλίου. Α.. Η διατύπωση του ορισμού βρίσκεται στη σελίδα 163 του σχολικού βιβλίου «εκθετική συνάρτηση». Α.3. i) Λάθος ii) Λάθος iii) Σωστό
ΘΕΜΑ Α Α.1. Η απόδειξη βρίσκεται στη σελίδα 175 του σχολικού βιβλίου. Α.. Η διατύπωση του ορισμού βρίσκεται στη σελίδα 163 του σχολικού βιβλίου «εκθετική συνάρτηση». Α.3. i) Λάθος ii) Λάθος iii) Σωστό
Η συνάρτηση y = αχ 2. Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd
 Η συνάρτηση y = αχ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y = αχ με α 0 Μια συνάρτηση της μορφής y = α + β + γ με α 0 ονομάζεται τετραγωνική συνάρτηση.
Η συνάρτηση y = αχ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y = αχ με α 0 Μια συνάρτηση της μορφής y = α + β + γ με α 0 ονομάζεται τετραγωνική συνάρτηση.
ΕΠΑΝΑΛΗΨΗ ΒΑΣΙΚΩΝ ΕΝΝΟΙΩΝ
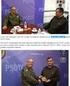 ΕΠΑΝΑΛΗΨΗ ΒΑΣΙΚΩΝ ΕΝΝΟΙΩΝ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμών αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
ΕΠΑΝΑΛΗΨΗ ΒΑΣΙΚΩΝ ΕΝΝΟΙΩΝ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμών αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ
 ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
x 1 δίνει υπόλοιπο 24
 ΓΕΝΙΚΕΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ 3. Δίνεται το πολυώνυμο P() 6 α β το οποίο έχει παράγοντα το και όταν διαιρείται με το δίνει υπόλοιπο i. Να δείξετε ότι: α και β 6 ii. Να λύσετε την εξίσωση
ΓΕΝΙΚΕΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ 3. Δίνεται το πολυώνυμο P() 6 α β το οποίο έχει παράγοντα το και όταν διαιρείται με το δίνει υπόλοιπο i. Να δείξετε ότι: α και β 6 ii. Να λύσετε την εξίσωση
ΜΕΡΟΣ Α. 1 ο ΚΕΦΑΛΑΙΟ
 ΜΕΡΟΣ Α ο ΚΕΦΑΛΑΙΟ. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών. Ονομάζεται αλγεβρική παράσταση μια παράσταση
ΜΕΡΟΣ Α ο ΚΕΦΑΛΑΙΟ. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών. Ονομάζεται αλγεβρική παράσταση μια παράσταση
ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ. ΘΕΜΑ 2ο
 ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β) Να παραστήσετε γραφικά
ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β) Να παραστήσετε γραφικά
Περιεχόμενα μεθόδευση του μαθήματος
 Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Ιωάννης Σ. Μιχέλης Μαθηματικός
 1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Ποιες είναι οι ιδιότητες της πρόσθεσης των φυσικών; Το άθροισμα ενός φυσικού αριθμού με το 0 ισούται με τον ίδιο αριθμό. α+0=α Αντιμεταθετική ιδιότητα. Με βάση την οποία
1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Ποιες είναι οι ιδιότητες της πρόσθεσης των φυσικών; Το άθροισμα ενός φυσικού αριθμού με το 0 ισούται με τον ίδιο αριθμό. α+0=α Αντιμεταθετική ιδιότητα. Με βάση την οποία
Κεφάλαιο 2 ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ
 Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
,, δηλαδή στο σημείο αυτό παρουσιάζει τη μέγιστη τιμή της αν α < 0 2α 4α και την ελάχιστη τιμή της αν α > 0. β Στο διάστημα,
 Γενικής Παιδείας 1.4 Εφαρμογές των παραγώγων Το κριτήριο της πρώτης παραγώγου Στην Άλγεβρα της Α Λυκείου μελετήσαμε τη συνάρτηση f(x) = αx + βx + γ, α 0 και είδαμε ότι η γραφική της παράσταση είναι μία
Γενικής Παιδείας 1.4 Εφαρμογές των παραγώγων Το κριτήριο της πρώτης παραγώγου Στην Άλγεβρα της Α Λυκείου μελετήσαμε τη συνάρτηση f(x) = αx + βx + γ, α 0 και είδαμε ότι η γραφική της παράσταση είναι μία
ΓΡΑΠΣΕ ΑΝΑΚΕΥΑΛΑΙΩΣΙΚΕ ΕΞΕΣΑΕΙ ΠΕΡΙΟΔΟΤ ΜΑΪΟΤ ΙΟΤΝΙΟΤ ΘΕΩΡΙΑ. Β. Να συμπληρώσετε στο γραπτό σας τις παρακάτω σχέσεις ώστε να προκύψουν ταυτότητες:
 ΓΡΑΠΣΕ ΑΝΑΚΕΥΑΛΑΙΩΣΙΚΕ ΕΞΕΣΑΕΙ ΠΕΡΙΟΔΟΤ ΜΑΪΟΤ ΙΟΤΝΙΟΤ ΣΑΞΗ: Γ ΘΕΩΡΙΑ ΘΕΜΑ 1 ο Α. Τι λέγεται ταυτότητα; Β. Να συμπληρώσετε στο γραπτό σας τις παρακάτω σχέσεις ώστε να προκύψουν ταυτότητες: Γ. Να αποδείξετε
ΓΡΑΠΣΕ ΑΝΑΚΕΥΑΛΑΙΩΣΙΚΕ ΕΞΕΣΑΕΙ ΠΕΡΙΟΔΟΤ ΜΑΪΟΤ ΙΟΤΝΙΟΤ ΣΑΞΗ: Γ ΘΕΩΡΙΑ ΘΕΜΑ 1 ο Α. Τι λέγεται ταυτότητα; Β. Να συμπληρώσετε στο γραπτό σας τις παρακάτω σχέσεις ώστε να προκύψουν ταυτότητες: Γ. Να αποδείξετε
Γραμμικά Συστήματα Δίνεται η εξίσωση 4x y 11(1). α) Ποια από τα ζεύγη (2, 3),(0, 11), (1, 8) κα (7, 0) είναι λύση της εξίσωσης (1);
 8808Δίνεται η εξίσωση x y 7 Γραμμικά Συστήματα α) Να επαληθεύσετε ότι το ζεύγος αριθμών x, y, είναι μια λύση της εξίσωσης β) Να αποδείξετε ότι το, 88Δίνεται η εξίσωση x y 8 δεν είναι λύση του συστήματος
8808Δίνεται η εξίσωση x y 7 Γραμμικά Συστήματα α) Να επαληθεύσετε ότι το ζεύγος αριθμών x, y, είναι μια λύση της εξίσωσης β) Να αποδείξετε ότι το, 88Δίνεται η εξίσωση x y 8 δεν είναι λύση του συστήματος
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ. ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ
 1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
θετικοί αριθμοί, να δείξετε ότι
 1 Ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΤΕΡΙΝΗΣ 9 /05/ 01 Προαγωγικές Εξετάσεις Β τάξης Εξεταζόμενο μάθημα : Άλγεβρα Σελίδες : (ΔΥΟ) ΘΕΜΑ 1 ο Α. Αν 0, 1 και, 1 θετικοί αριθμοί, να δείξετε ότι log a 1 log 1 log (15 μονάδες)
1 Ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΤΕΡΙΝΗΣ 9 /05/ 01 Προαγωγικές Εξετάσεις Β τάξης Εξεταζόμενο μάθημα : Άλγεβρα Σελίδες : (ΔΥΟ) ΘΕΜΑ 1 ο Α. Αν 0, 1 και, 1 θετικοί αριθμοί, να δείξετε ότι log a 1 log 1 log (15 μονάδες)
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Γραμμικά Συστήματα. δεν είναι λύση του συστήματος. β) Ποιο από τα παραπάνω ζεύγη είναι λύση του συστήματος
 8808Δίνεται η εξίσωση x y 7 Γραμμικά Συστήματα α) Να επαληθεύσετε ότι το ζεύγος αριθμών x, y 4, είναι μια λύση της εξίσωσης β) Να αποδείξετε ότι το 4, 88Δίνεται η εξίσωση x y 8 δεν είναι λύση του συστήματος
8808Δίνεται η εξίσωση x y 7 Γραμμικά Συστήματα α) Να επαληθεύσετε ότι το ζεύγος αριθμών x, y 4, είναι μια λύση της εξίσωσης β) Να αποδείξετε ότι το 4, 88Δίνεται η εξίσωση x y 8 δεν είναι λύση του συστήματος
1.1 ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ (Επαναλήψεις Συμπληρώσεις) Τριγωνομετρικοί αριθμοί οξείας γωνίας
 . ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ (Επαναλήψεις Συμπληρώσεις) Τριγωνομετρικοί αριθμοί οξείας γωνίας Έστω οξεία γωνία ω. Αν πάνω στη μία από τις δύο πλευρές της γωνίας πάρουμε τυχαία σημεία Μ και Ν και φέρουμε
. ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ (Επαναλήψεις Συμπληρώσεις) Τριγωνομετρικοί αριθμοί οξείας γωνίας Έστω οξεία γωνία ω. Αν πάνω στη μία από τις δύο πλευρές της γωνίας πάρουμε τυχαία σημεία Μ και Ν και φέρουμε
α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν β) γνησίως φθίνουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.
 ΜΟΝΟΤΟΝΙΑ. ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ Μια συνάρτηση f λέγεται: α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν για οποιαδήποτε χ,χ Δ με χ
ΜΟΝΟΤΟΝΙΑ. ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ. ΜΟΝΟΤΟΝΙΑ - ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ Μια συνάρτηση f λέγεται: α) γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της (Σχ.α), όταν για οποιαδήποτε χ,χ Δ με χ
ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ 6 Β' Λυκείου. Ύλη: Συστήματα Ιδιότητες Συναρτήσεων- Τριγωνομετρία
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ 6 Β' Λυκείου Ον/μο:. ΕΠΑ.Λ. Ύλη: Συστήματα Ιδιότητες Συναρτήσεων- Τριγωνομετρία 06-11-16 Θέμα 1 ο : Α.i. Τι ονομάζουμε γραμμική εξίσωση; (4 μον.) ii. Πότε μία συνάρτηση f ονομάζεται
ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ 6 Β' Λυκείου Ον/μο:. ΕΠΑ.Λ. Ύλη: Συστήματα Ιδιότητες Συναρτήσεων- Τριγωνομετρία 06-11-16 Θέμα 1 ο : Α.i. Τι ονομάζουμε γραμμική εξίσωση; (4 μον.) ii. Πότε μία συνάρτηση f ονομάζεται
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
